In this example, if we had replaced the zeros below the main diagonal with the ratio of coefficients at each step, the resulting augmented matrix would be
This gives a LU decomposition as
It should be noted that the product or the matrices produces a permutation of the original matrix, call it 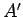 , where
The determinant of the original matrix of coefficients can be easily computed according to the formula
which is close to the exact solution: -234. The exponent 2 is required, because there were two row interchanges in solving this system. To summarize
, where
The determinant of the original matrix of coefficients can be easily computed according to the formula
which is close to the exact solution: -234. The exponent 2 is required, because there were two row interchanges in solving this system. To summarize
- The solution to the four equations
- The determinant of the coefficient matrix
- A
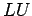 decomposition of the matrix,
decomposition of the matrix, 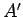 , which is just the original matrix,
, which is just the original matrix, 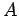 , after we have interchanged its rows in the process.
, after we have interchanged its rows in the process.
>> A = [0 2 0 1 0 ; 2 2 3 2 -2 ; 4 -3 0 1 -7 ; 6 1 -6 -5 6]
>> [L, U, P]=lu(A)
>> b = [ 0 -2 -7 6]
>> A\b
ans =
-0.5000
1.0000
0.3333
-2.0000
![\begin{displaymath}
\left[
\begin{array}{rrrr}
4 & -2 & 1 &15 \\
-3 & -1 & 4 ...
...75 &19.25 \\
0 & -0.5 & 2.75 & 9.25 \\
\end{array} \right],
\end{displaymath}](img415.png)
![\begin{displaymath}
\begin{array}{r}
\\
\\
R_3-(-0.5/-2.5)R_2 \rightarrow \...
...& 4.75 & 19.25 \\
0 & 0 & 1.8 & 5.40 \\
\end{array} \right]
\end{displaymath}](img416.png)
![\begin{displaymath}
\left[
\begin{array}{rrrr}
4 & -2 & 1 &15 \\
(-0.75) & -2...
...9.25 \\
(0.25) & (0.20) & 1.8 & 5.40 \\
\end{array} \right]
\end{displaymath}](img417.png)
![\begin{displaymath}
A=\underbrace{\left[
\begin{array}{rrr}
1 & 0 & 0 \\
-0.7...
...
0 & -2.5 & 4.75 \\
0 & 0 & 1.8 \\
\end{array} \right]}_U
\end{displaymath}](img418.png)
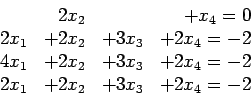
![\begin{displaymath}
\left[
\begin{array}{rrrrr}
0 & 2 & 0 & 1 &0 \\
2 & 2 & 3...
...& -3 & 0 & 1 &-7 \\
6 & 1 &-6 &-5 &6 \\
\end{array} \right]
\end{displaymath}](img427.png)
![\begin{displaymath}
\left[
\begin{array}{rrrrr}
6 & 1 &-6 &-5 &6 \\
2 & 2 & 3...
...& -3 & 0 & 1 &-7 \\
0 & 2 & 0 & 1 &0 \\
\end{array} \right]
\end{displaymath}](img429.png)
![\begin{displaymath}
\left[
\begin{array}{rrrrr}
6 & 1 &-6 &-5 &6 \\
0 &1.6667...
... & 4 &4.3333&-11 \\
0 & 2 & 0 & 1 &0 \\
\end{array} \right]
\end{displaymath}](img430.png)
![\begin{displaymath}
\left[
\begin{array}{rrrrr}
6 & 1 &-6 &-5 &6 \\
0 &-3.666...
...67& 5 &3.6667&-4 \\
0 & 2 & 0 & 1 &0 \\
\end{array} \right]
\end{displaymath}](img431.png)
![\begin{displaymath}
\left[
\begin{array}{rrrrr}
6 & 1 &-6 &-5 &6 \\
0 &-3.666...
...1\\
0 & 0 & 2.1818 & 3.3636 &-5.9999 \\
\end{array} \right]
\end{displaymath}](img432.png)
![\begin{displaymath}
\left[
\begin{array}{rrrrr}
6 & 1 &-6 &-5 &6 \\
0 &-3.666...
...9.0001\\
0 & 0 & 0 & 1.5600 &-3.1199 \\
\end{array} \right]
\end{displaymath}](img433.png)
![\begin{displaymath}
\left[
\begin{array}{rrrrr}
6 & 1 &-6 &-5 &6 \\
(0.66667)...
... (-0.54545) & (0.32) & 1.5600 &-3.1199 \\
\end{array} \right]
\end{displaymath}](img436.png)
![\begin{displaymath}
\left[
\begin{array}{rrrr}
1&0&0&0\\
0.66667 & 1 & 0 & 0 ...
... & 6.8182 &5.6364\\
0& 0 &0 & 1.5600 \\
\end{array} \right]
\end{displaymath}](img437.png)
![\begin{displaymath}
A'=\left[
\begin{array}{rrrr}
6 & 1 &-6 &-5 \\
4 & -3 & 0...
... \\
2 & 2 & 3 & 2 \\
0 & 2 & 0 & 1 \\
\end{array} \right]
\end{displaymath}](img439.png)