- Many physical situations are modelled with a large set of linear equations.
- The equations will depend on the geometry and certain external factors that will determine the right-hand sides.
- If we want the solution for many different values of these right-hand sides, it is inefficient to solve the system from the start with each one of the right-hand-side values using the
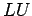 equivalent of the coefficient matrix is preferred.
equivalent of the coefficient matrix is preferred.
- Suppose we have solved the system
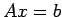 by Gaussian elimination. We now know the
by Gaussian elimination. We now know the 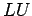 equivalent of A:
equivalent of A: 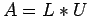 .
.
- Consider now that we want to solve
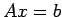 with some new
with some new 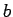 -vector. We can write
-vector. We can write
- The product of
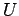 and
and 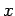 is a vector, call it
is a vector, call it 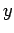 . Now, we can solve for
. Now, we can solve for 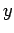 from
from 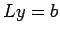 and this is readily done because
and this is readily done because 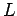 is lower-triangular and we get
is lower-triangular and we get 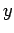 by forward-substitution. Call the solution
by forward-substitution. Call the solution 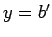 .
.
- Going back to the original
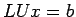 , we see that, from
, we see that, from 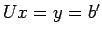 , we can get
, we can get 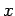 from
from 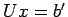 , which is again readily done by back-substitution (
, which is again readily done by back-substitution (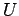 is upper-triangular).
is upper-triangular).
- i.e., Solve
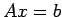 , where we already have its
, where we already have its 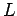 and
and 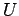 matrices:
Suppose that the
matrices:
Suppose that the 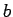 -vector is
-vector is
![$ [6, -7, -2, 0]^T$](img454.png) . We first get
. We first get 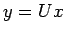 from
from 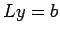 by forward substitution:
and use it to compute
by forward substitution:
and use it to compute 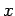 from
from 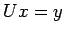 :
:
- Now, if we want the solution with a different
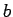 -vector;
we just do
-vector;
we just do 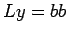 to get
and then use this
to get
and then use this 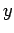 in
in 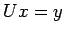 to find the new
to find the new 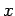 :
:
2004-12-28
![\begin{displaymath}
\left[
\begin{array}{rrrr}
1&0&0&0\\
0.66667 & 1 & 0 & 0 ...
... & 6.8182 &5.6364\\
0& 0 &0 & 1.5600 \\
\end{array} \right]
\end{displaymath}](img437.png)