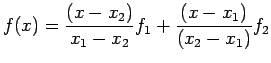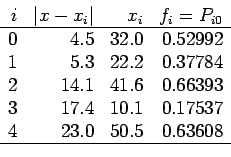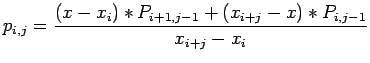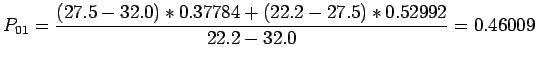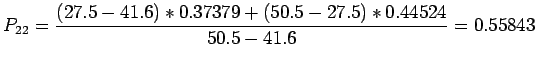Neville's Method
- The trouble with the standard Lagrangian polynomial technique is that we do not know which degree of polynomial to use.
- If the degree is too low, the interpolating polynomial does not give good estimates of
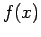 .
.
- If the degree is too high, undesirable oscillations in polynomial values can occur.
- Neville's method can overcome this difficulty. It computes the interpolated value with polynomials of successively higher degree, stopping when the successive values are close together.
- The successive approximations are actually computed by linear interpolation from the previous values. The Lagrange formula for linear interpolation to get
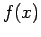 from two data pairs,
from two data pairs, 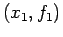 and
and 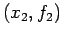 , is
, is
- Neville's method begins by arranging the given data pairs,
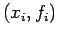 , so the successive values are in order of the closeness of the
, so the successive values are in order of the closeness of the 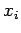 to
to 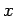 .
.
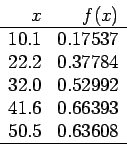
- Suppose we are given these data
and we want to interpolate for
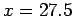 . We first rearrange the data pairs in order of closeness to
. We first rearrange the data pairs in order of closeness to 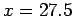 :
Neville's method begins by renaming the
:
Neville's method begins by renaming the 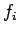 as
as 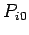 . We build a table
The general formula for computing entries into the table is
Thus, the value of
. We build a table
The general formula for computing entries into the table is
Thus, the value of 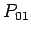 is computed by '
Once we have the column of
is computed by '
Once we have the column of 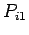 's, we compute the next column.
The remaining columns are computed similarly.
's, we compute the next column.
The remaining columns are computed similarly.
The top line of the table represents Lagrangian interpolates at 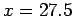 using polynomials of degree equal to the second subscript of the
using polynomials of degree equal to the second subscript of the 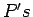 .
.
- The preceding data are for sines of angles in degrees and the correct value for
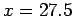 is
is 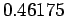 .
.
2004-12-28