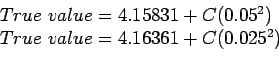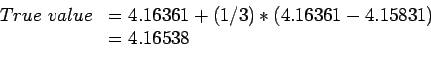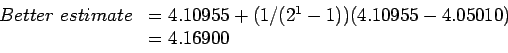Extrapolation Techniques
- The errors of a central-difference approximation to
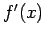 were of
were of 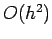 . In effect, suggests that the errors are proportional to
. In effect, suggests that the errors are proportional to 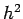 although that is true only in the limit as
although that is true only in the limit as
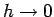 . Unless
. Unless 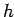 is quite large, we can assume the proportionality.
is quite large, we can assume the proportionality.
- So, from two computations with
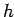 being half as large in the second, we can estimate the proportionality factor,
being half as large in the second, we can estimate the proportionality factor, 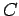 . For example, in Table 7.2;
. For example, in Table 7.2;
| h |
Approximation |
| 0.05 |
4.15831 |
| 0.025 |
4.16361 |
If errors were truly 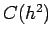 , we can write two equations:
from which we can solve for the true value, eliminating the unknown constant
, we can write two equations:
from which we can solve for the true value, eliminating the unknown constant 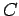 , getting;
which is very close to the exact value for
, getting;
which is very close to the exact value for 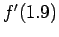 , 4.165382.
, 4.165382.
- You can easily derive the general formula for improving the estimate, when errors decrease by
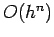
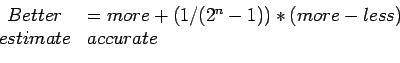 |
(7.4) |
where more and less in the last term are the two estimates at 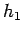 and
and 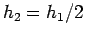 . More accurate is the estimate at the smaller value of
. More accurate is the estimate at the smaller value of 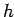 and
and 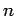 is the power of
is the power of 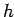 in the order of the errors.
in the order of the errors.
- As example, apply this to values from Table 7.1 which were from forward-difference approximations. Here the errors are
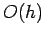 .
.
| h |
Approximation |
| 0.05 |
4.05010 |
| 0.025 |
4.10955 |
Using Eq. 7.4, we have
which shows considerable improvement but not as good as from the central differences.
2004-12-28