Ceng 375 Numerical Computing
Final
Jan 14, 2005 09.40-11.30
Good Luck!
1 (20 Pts)
- IV
- In Newton's method the approximation
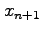 to a root of
to a root of 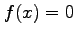 is computed from the approximation
is computed from the approximation 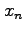 using the equation
using the equation
Derive the above formula, using a Taylor series of 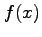 .
.
- V
- Consider the function:
- i
- Show that this function has a simple root in the interval
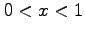
- ii
- Estimate this root using two iterations of the Secant Method.
- iii
- Estimate the error in your answer to part ii.
2 (20 Pts) Solve this system by Gaussian elimination with pivoting
- vi
- How many row interchanges are needed?
- vii
- Repeat without any row interchanges. Do you get the same results?
- viii
- You could have saved the row multipliers and obtained a
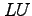 equivalent of the coefficient matrix. Use this
equivalent of the coefficient matrix. Use this 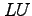 to solve but with right-hand sides of
to solve but with right-hand sides of ![$[1,-3,5]^T$](img10.png)
3 (25 Pts)
- ix
- A function
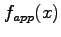 is to be used as an approximation to a set of data
is to be used as an approximation to a set of data 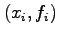 with
with
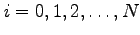 . Suppose further that the function
. Suppose further that the function 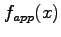 depends on two parameters
depends on two parameters 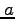 and
and 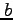 . Provide full details of how the parameters
. Provide full details of how the parameters 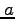 and
and 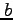 can be determined by a Least Squares Method.
can be determined by a Least Squares Method.
- x
- Using the result of the previous item, obtain the normal equations for the function
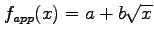 . Do not attempt to solve these equations.
. Do not attempt to solve these equations.
4 (20 Pts)
- xi
- Find the Fourier coefficients for
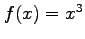 if it is periodic and one period extends from
if it is periodic and one period extends from 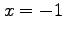 to
to 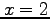 .
.
- xii
- Write the Fourier series for this function.
5 (25 Pts) Consider the following table of data
 |
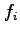 |
| 0.0000 |
0.0000 |
| 0.2000 |
0.5879 |
| 0.4000 |
1.0637 |
| 0.6000 |
1.3927 |
| 0.8000 |
1.5573 |
| 1.0000 |
1.5575 |
| 1.2000 |
1.4091 |
- xiii
- Approximate
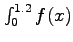 dx using the Trapezoidal Rule and a step size of
dx using the Trapezoidal Rule and a step size of 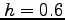 .
.
- xiv
- Approximate
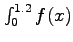 dx using the Trapezoidal Rule and a step size of
dx using the Trapezoidal Rule and a step size of 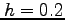 .
.
- xv
- Estimate the error in your answer to previous item.
Hint: Use the procedure to estimate the proportionality factor, 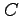 .
.
2006-09-28
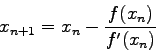
![\begin{displaymath}
\left[
\begin{array}{rrrr}
1 &-2 &4&6\\
8 &-3 &2&2\\
-1 &10 &2&4\\
\end{array} \right]
\end{displaymath}](img8.png)