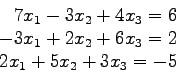Ceng 375 Numerical Computing
Midterm
Nov 9, 2004 13.40-15.30
Good Luck!
1 (15 Pts) In Newton's method the approximation 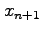 to a root of
to a root of 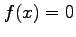 is computed from the approximation
is computed from the approximation 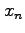 using the equation
using the equation
- i
- Derive the above formula, using a Taylor series of
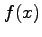 .
.
- ii
- For
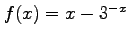 , refine the approximation
, refine the approximation 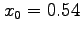 to the unique root of
to the unique root of 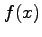 by carrying out one iteration of Newton's method.
by carrying out one iteration of Newton's method.
Hints:
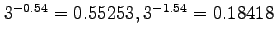 2 (15 Pts) Consider the function:
2 (15 Pts) Consider the function:
- iii
- Show that this function has a simple root in the interval
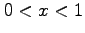
- iv
- Estimate this root using two iterations of the Secant Method.
- v
- Estimate the error in your answer to part ii.
- vi
- Would Newton's method have been preferable in this problem? (Briefly explain your answer!)
Hints:
 3 (15 Pts) Illustrate graphically the cases of monotonic convergence, oscillatory convergence and divergence for the fixed-point (
3 (15 Pts) Illustrate graphically the cases of monotonic convergence, oscillatory convergence and divergence for the fixed-point (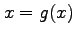 ) iteration method.
) iteration method.
4 (15 Pts) Let
- vii
- Find the characteristic polynomials of both
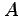 and
and 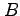 .
.
- viii
- Find the eigenvalues of both
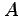 and
and 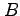 .
.
- ix
- Is
![$[0.2104,0.8401]$](img16.png) an eigenvector of
an eigenvector of 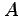 ?
?
5 (20 Pts) Solve this system by Gaussian elimination with pivoting
- x
- How many row interchanges are needed?
- xi
- Repeat without any row interchanges. Do you get the same results?
- xii
- You could have saved the row multipliers and obtained a
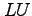 equivalent of the coefficient matrix. Use this
equivalent of the coefficient matrix. Use this 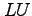 to solve but with right-hand sides of
to solve but with right-hand sides of ![$[1,-3,5]^T$](img19.png)
6 (20 Pts) Consider the matrix
- xiii
- Use the Gaussian elimination method to triangularize this matrix and from that gets its determinant.
- xiv
- Get the inverse of the matrix through Gaussian elimination.
- xv
- Get the inverse of the matrix through Gauss-Jordan method.
7 (20 Pts) Consider the linear system
- xvi
- Solve this system with the Jacobi method. First rearrange to make it dioganally dominant if possible. Use
![$[0,0,0]$](img22.png) as the starting vector. Proceed only 1 iteration.
as the starting vector. Proceed only 1 iteration.
- xvii
- Repeat with Gauss-Seidel method. Compare with Jacobi method.
2006-09-28
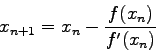
![\begin{displaymath}
A=\left[
\begin{array}{rr}
2 & 9 \\
3 &-10\\
\end{array}...
... & 6 & 2 \\
4 &-1 & 3 \\
1 &-3 &-1 \\
\end{array} \right]
\end{displaymath}](img13.png)
![\begin{displaymath}
\left[
\begin{array}{rrrr}
1 &-2 &4&6\\
8 &-3 &2&2\\
-1 &10 &2&4\\
\end{array} \right]
\end{displaymath}](img17.png)
![\begin{displaymath}
A=\left[
\begin{array}{rrr}
3 &-1 &2\\
1 & 1 &3\\
-3 & 0 &5\\
\end{array} \right]
\end{displaymath}](img20.png)