Figure 4:
Left: The curve on the left has a triple root at 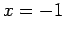 [the function is
[the function is 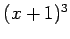 ]. The curve on the right has a double root at
]. The curve on the right has a double root at 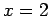 [the function is
[the function is 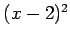 ].Right: Plot of
].Right: Plot of
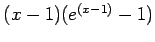 .
.
|
- A function can have more than one root of the same value. See Fig. 4left.
- The methods we have described do not work well for multiple roots. For example, Newton's method is only linearly convergent at a double root.
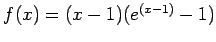 has a double root at
has a double root at 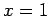 , as seen in Fig. 4right.
, as seen in Fig. 4right.
- Table 2left gives the errors of successive iterates and the convergence is clearly linear.
- When Newton's method is applied to a triple root, convergence is still linear, as seen in Table 2right. With a triple root, the ratio of errors is larger, about
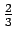 , compared to
, compared to 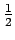 for the double root of Table 2left.
for the double root of Table 2left.
Table 2:
Right: Errors when finding a double root. Left: Successive errors with Newton's method, for
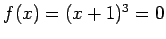 .
.
![\includegraphics[scale=0.85]{figures/1.18.ps}](img71.png) |
![\includegraphics[scale=0.85]{figures/1.19.ps}](img72.png) |
2004-10-18
![\includegraphics[scale=0.85]{figures/1.18.ps}](img71.png)
![\includegraphics[scale=0.85]{figures/1.19.ps}](img72.png)