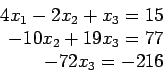Elimination Methods
- To solve a set of linear equations. The term linear equation means an equation in several variables where all of the variables occur to the first power.
- Suppose we have a system of equations that is of a special form, an upper-triangular system, such as
we have the solution
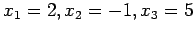
- The first objective of the elimination method is to change the matrix of coefficients so that it is upper triangular. Consider this example of three equations:
Now we have a triangular system and the solution is readily obtained; obviously 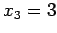 from the third equation, and back-substitution into the second equation gives
from the third equation, and back-substitution into the second equation gives 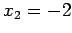 . We continue with back-substitution by substituting both
. We continue with back-substitution by substituting both 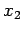 , and
, and 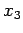 into the first equation to get
into the first equation to get 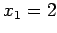 .
.
- The essence of any elimination method is to reduce the coefficient matrix to a triangular matrix and then use back-substitution to get the solution.
- We now present the same problem, solved in exactly the same way, in matrix notation;
- The arithmetic operations that we have performed affect only the coefficients and the right-hand-side terms, so we work with the matrix of coefficients augmented with the right-hand-side vector.
- We perform elementary row transformations to convert A to upper-triangular form:
- This array represents the equations
The back-substitution step can be performed quite mechanically by solving the equations in reverse order. That is,
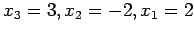 .
.
- Both the lower-and upper-triangular systems play an important part in the development of algorithms in the following sections, because these systems require fewer multiplications/divisions than the general system.
- Note that there exists the possibility that the set of equations has no solution, or that the prior procedure will fail to find it.
- During the triangularization step, if a zero is encountered on the diagonal, we cannot use that row to eliminate coefficients below that zero element. However, in that case, we can continue by interchanging rows and eventually achieve an upper-triangular matrix of coefficients.
- The real trouble is finding a zero on the diagonal after we have triangularized. If that occurs, the back-substitution fails, for we cannot divide by zero. It a1so means that the determinant is zero. There is no solution.
Subsections
2004-11-03
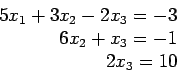
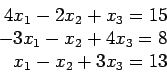
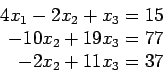
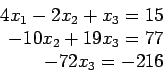
![\begin{displaymath}
\left[
\begin{array}{rrr}
4 & -2 & 1 \\
-3 & -1 & 4 \\
...
...t[
\begin{array}{r}
15 \\
8 \\
13 \\
\end{array} \right]
\end{displaymath}](img70.png)
![\begin{displaymath}
\left[
\begin{array}{rrrr}
4 & -2 & 1 &15 \\
-3 & -1 & 4 ...
...0 & -10 & 19 &77 \\
0 & -2 & 11 &37 \\
\end{array} \right],
\end{displaymath}](img71.png)
![\begin{displaymath}
\begin{array}{r}
\\
\\
2R_2-10R_3 \rightarrow \\
\end{...
...0 & -10 & 19 &77 \\
0 & 0 & 72 &-216 \\
\end{array} \right]
\end{displaymath}](img72.png)