| For Singular matrix A: |
For Nonsingular Matrix A: |
It has no inverse, 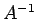 |
It has an inverse, 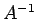 |
| Its determinant is zero |
The determinant is nonzero |
| There is no unique solution |
There is a unique solution |
to the system 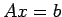 |
to the system 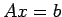 |
| Gaussian elimination cannot avoid |
Gaussian elimination does not |
| a zero on the diagonal |
encounter a zero on the diagonal |
The rank is less than 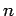 |
The rank equals 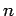 |
| Rows are linearly dependent |
Rows are linearly independent |
| Columns are linearly dependent |
Columns are linearly independent |
![\begin{displaymath}
A=\left[
\begin{array}{rrr}
1 & -2 & 3 \\
2 & 4 &-1 \\
-1 &-14 & 11\\
\end{array} \right]
\end{displaymath}](img17.png)