Next: About this document ... Up: week6l Previous: week6l
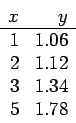
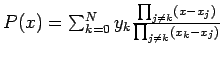 based on
based on
function [C,L]=lagran(X,Y)
%Input - X is a vector that contains a list of abscissas
% - Y is a vector that contains a list of ordinates
%Output - C is a matrix that contains the coefficents of
% the Lagrange interpolatory polynomial
% - L is a matrix that contains the Lagrange coefficient polynomials
w=length(X);
n=w-1;
L=zeros(w,w);
%Form the Lagrange coefficient polynomials
for k=1:n+1
V=1;
for j=1:n+1
if k~=j
V=conv(V,poly(X(j)))/(X(k)-X(j));
end
end
L(k,:)=V;
end
%Determine the coefficients of the Lagrange interpolator polynomial
C=Y*L;
where
>>P=poly(2) >> 1 -2 >>Q=poly(3) >> 1 -3
>>conv(P,Q) >> 1 -5 6 %Thus the product of P(x) and Q(x) is x^2-5x+6
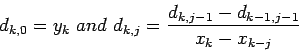
function [C,D]=newpoly(X,Y)
%Input - X is a vector that contains a list of abscissas
% - Y is a vector that contains a list of ordinates
%Output - C is a vector that contains the coefficients
% of the Newton interpolatory polynomial
% - D is the divided difference table
n=length(X);
D=zeros(n,n);
D(:,1)=Y';
%Use the formula above to form the divided difference table
for j=2:n
for k=j:n
D(k,j)=(D(k,j-1)-D(k-1,j-1))/(X(k)-X(k-j+1));
end
end
%Determine the coefficients of the Newton interpolatory polynomial
C=D(n,n);
for k=(n-1):-1:1
C=conv(C,poly(X(k)));
m=length(C);
C(m)=C(m)+D(k,k);
end
Study this MATLAB code and then use the data set in the first item to