The Equation for a Cubic Spline
- We will create a succession of cubic splines over successive intervals of the data (See Fig. 4). Each spline must join with its neighboring cubic polynomials at the knots where they join with the same slope and curvature.
- We write the equation for a cubic polynomial,
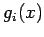 , in the
, in the 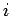 th interval, between points
th interval, between points
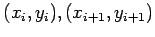 . It looks like the solid curve shown here. The dashed curves are other cubic spline polynomials. It has this equation:
. It looks like the solid curve shown here. The dashed curves are other cubic spline polynomials. It has this equation:
Thus, the cubic spline function we want is of the form
and meets these conditions:
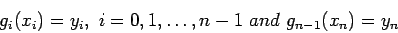 |
(1) |
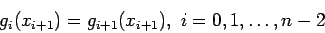 |
(2) |
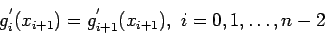 |
(3) |
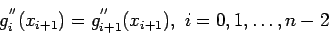 |
(4) |
- Equations say that the cubic spline fits to each of the points Eq. 1, is continuous Eq. 2, and is continuous in slope and curvature Eq. 3 and Eq. 4, throughout the region spanned by the points.
2004-12-06