


Next: About this document ...
Ceng 375 Numerical Computations
Final
Jan 15, 2007 14.00-16.00
Good Luck!
- (25 Pts) Consider the solution to
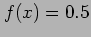 where
where 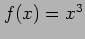 . Choosing initial guesses of
. Choosing initial guesses of 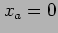 and
and 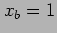 ,
,
- i
- Write down an expression to show how the error en in the bisection method decreases with subsequent iterations.
- ii
- Using the bisection method, determine the solution to four decimal places. Does the number of iterations this took agree with the predicted number?
- (25 Pts)
- iii
- A function
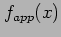 is to be used as an approximation to a set of data
is to be used as an approximation to a set of data 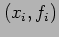 with
with
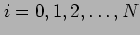 . Suppose further that the function
. Suppose further that the function 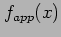 depends on two parameters
depends on two parameters 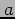 and
and 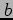 . Provide full details of how the parameters
. Provide full details of how the parameters 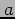 and
and 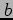 can be determined by a Least Squares Method.
can be determined by a Least Squares Method.
- iv
- Using the result of the previous item, obtain the normal equations for the function
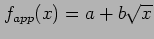 . Do not attempt to solve these equations.
. Do not attempt to solve these equations.
- (25 Pts)
- v
- Find the Fourier coefficients for
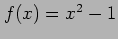 if it is periodic and one period extends from
if it is periodic and one period extends from 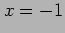 to
to  . Do not evaluate the integrals.
. Do not evaluate the integrals.
- vi
- Write the Fourier series expansion for this function up to
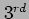 term.
term.
- (25 Pts) Consider the function
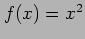 ;
;
- vii
- Fill the following table within the five digit accuracy
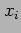 |
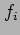 |
| 0.00000 |
0.00000 |
| |
|
| |
|
| |
|
| |
|
| |
|
| 1.20000 |
|
- viii
- Approximate
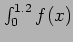 dx using the Trapezoidal Rule and a step size of
dx using the Trapezoidal Rule and a step size of 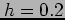 .
.
- ix
- Approximate
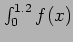 dx using the Trapezoidal Rule and a step size of
dx using the Trapezoidal Rule and a step size of 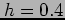 .
.
- x
- Analyze and compare your results. Estimate the error in your answers.



Next: About this document ...
Cem Ozdogan
2007-11-20
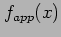 is to be used as an approximation to a set of data
is to be used as an approximation to a set of data 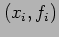 with
with
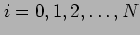 . Suppose further that the function
. Suppose further that the function 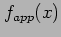 depends on two parameters
depends on two parameters 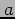 and
and 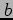 . Provide full details of how the parameters
. Provide full details of how the parameters 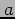 and
and 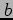 can be determined by a Least Squares Method.
can be determined by a Least Squares Method.
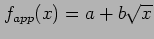 . Do not attempt to solve these equations.
. Do not attempt to solve these equations.
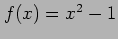 if it is periodic and one period extends from
if it is periodic and one period extends from 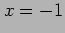 to
to  . Do not evaluate the integrals.
. Do not evaluate the integrals.
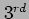 term.
term.
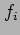
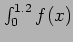 dx using the Trapezoidal Rule and a step size of
dx using the Trapezoidal Rule and a step size of 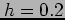 .
.
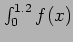 dx using the Trapezoidal Rule and a step size of
dx using the Trapezoidal Rule and a step size of 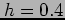 .
.