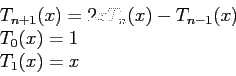Ceng 375 Numerical Computing
Final
Jan 15, 2009 13.00-15.00
Good Luck!
- (10pts) Choose only two questions.
- i
- What are the advantages and disadvantages of numerical analysis?
- ii
- Describe truncation and round-off errors. Give example.
- iii
- Describe the concept of ill-conditionness. Give an example.
- iv
- What information can be obtained from the determinant of a matrix?
- v
- Why do we need pivoting while solving sets of equations by elimination methods? Can we skip pivoting and under which circumstances?
- vi
- What does singularity mean for a matrix? Make a comparison of singular and nonsingular matrices.
- vii
- What information can be obtained from the condition number of a matrix?
- viii
- What are the differences between the interpolation and curve fitting?
- (20pts) Choose only two questions.
- ix
- For the given data points;
we suggest the relation
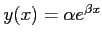 .
.
- First, construct the normal equations.
- Then, describe the remaining steps.
- x
- Solve the following linear system by either by Jacobi or Gauss-Seidel iterations;
- Start by
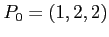 . Iterate only two steps.
. Iterate only two steps.
- Compare Jacobi or Gauss-Seidel methods.
- xi
- Consider the function:
- Show that this function has a simple root in the interval
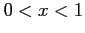
- Estimate this root using two iterations of the Secant Method. The secant algorithm is
- Estimate the error in your answer to part ii.
- (20pts) Consider the matrix
- xii
- Use the Gaussian elimination method to triangularize this matrix and from that gets its determinant.
- xiii
- Get the inverse of the matrix through Gauss-Jordan method.
- (20pts)
- xiv
- Find the Fourier coefficients for
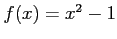 if it is periodic and one period extends from
if it is periodic and one period extends from 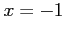 to
to  . Do not evaluate the integrals.
. Do not evaluate the integrals.
- xv
- Write the Fourier series expansion for this function until
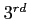 term.
term.
- (20pts) Write the expression to economize the the Maclaurin series for
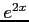 with the precision 0.008 by using Chebyshev polynomials.
with the precision 0.008 by using Chebyshev polynomials.
Hint: The two-term recursion formula
- (20pts) Consider the function
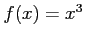 . Following table within the five digit accuracy is given.
. Following table within the five digit accuracy is given.
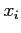 |
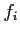 |
| 0.00000 |
0.00000 |
| 0.20000 |
0.00800 |
| 0.40000 |
0.06400 |
| 0.60000 |
0.21600 |
| 0.80000 |
0.51200 |
| 1.00000 |
1.00000 |
| 1.20000 |
1.72800 |
- xvi
- Approximate
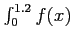 dx using the Trapezoidal Rule and a step size of
dx using the Trapezoidal Rule and a step size of 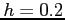 .
.
- xvii
- Approximate
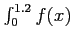 dx using the Trapezoidal Rule and a step size of
dx using the Trapezoidal Rule and a step size of 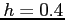 .
.
- xviii
- Estimate the error in your answers;
- Find the exact value of the integral simply by integrating the given function. Then, find the errors for parts i and ii.
- Also use the following global error formula to find the errors for parts i and ii.
- Analyze and compare these error values.
Cem Ozdogan
2010-06-15
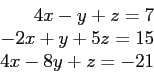
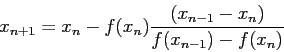
![\begin{displaymath}
A=\left[
\begin{array}{rrr}
3 &-1 &2\\
1 & 1 &3\\
-3 & 0 &5\\
\end{array} \right]
\end{displaymath}](img7.png)