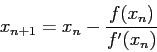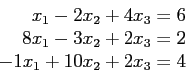The following function is given
This nonlinear equation (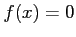 ) is solved by using four methods, namely Bisection, Regula Falsi, Newton's, Muller's methods. See the following MATLAB commands;
) is solved by using four methods, namely Bisection, Regula Falsi, Newton's, Muller's methods. See the following MATLAB commands;
>> f = inline ( ' 2*sin( x) - exp ( x)/4 -1');
>> df = inline ( ' 2*cos( x) - exp ( x)/4');
>> fplot(f,[-7 -3]); grid on;
>> format short e
>> bisect(f,-7,-5,fzero(f,[-7 -5]),1e-5);
>> regula(f,-7,-5,fzero(f,[-7 -5]),1e-5,eps,20);
>> newton(f,df,-7,fzero(f,[-7 -5]),1e-5,eps,20);
>> muller(f,-7,-6,-5,fzero(f,[-7 -5]),1e-5,eps,20);
Plot of the function is given at the following figure;
Then, the following tables are obtained.
Table:
Obtained root values at each iteration for all of four methods.
| iteration |
Bisection |
Regula |
Newton |
Muller |
| 1 |
-6.0000e+00 |
-5.5672e+00 |
-5.4650e+00 |
-5.7134e+00 |
| 2 |
5.5000e+00 |
-5.7373e+00 |
-5.8008e+00 |
-5.7604e+00 |
| 3 |
-5.7500e+00 |
-5.7575e+00 |
-5.7596e+00 |
-5.7591e+00 |
| 4 |
-5.8750e+00 |
-5.7590e+00 |
-5.7591e+00 |
-5.7591e+00 |
| 5 |
-5.8125e+00 |
-5.7591e+00 |
-5.7591e+00 |
- |
| 6 |
-5.7812e+00 |
-5.7591e+00 |
- |
- |
Table:
Obtained function values at each iteration for all of four methods.
| iteration |
Bisection |
Regula |
Newton |
Muller |
| 1 |
-4.4179e-01 |
3.1174e-01 |
4.5882e-01 |
7.8084e-02 |
| 2 |
4.1006e-01 |
3.7524e-02 |
-7.3051e-02 |
-2.2184e-03 |
| 3 |
1.5762e-02 |
2.8928e-03 |
-8.1042e-04 |
4.1882e-06 |
| 4 |
-2.0681e-01 |
2.0926e-04 |
-1.0968e-07 |
-4.0674e-11 |
| 5 |
-9.3753e-02 |
1.5061e-05 |
-2.2204e-15 |
- |
| 6 |
-3.8525e-02 |
1.0836e-06 |
- |
- |
- i
- Analyze these tables. Is the convergence sustained for the each methods? For the sustained ones; at which iteration and why?
- ii
- If the exact value is given as
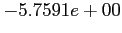 , fill the following table for two methods. Choose two methods and use scientific notation with five significant figures.;
, fill the following table for two methods. Choose two methods and use scientific notation with five significant figures.;
- iii
- What can you say about the speed of convergences for each method?
- iv
- Which method is the best one? Why?