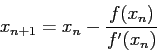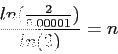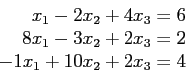Ceng 375 Numerical Computing
Midterm
Nov 12, 2009 14.40-16.30
Good Luck!

Each question is 25 pts.

1. The following function is given
   
   $$f(x)=3*sin(x)- e^x/4-1$$
   
   
   This nonlinear equation (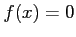$f(x)=0$) is solved by using four methods, namely Bisection, Regula Falsi, Newton's, Muller's methods. See the following MATLAB commands;

   >> f = inline ( ' 3*sin( x) - exp ( x)/4 -1');
   >> df = inline ( ' 3*cos( x) - exp ( x)/4');
   >> fplot(f,[-7 -3]); grid on;
   >> format short e
   >> bisect(f,-7,-5,fzero(f,[-7 -5]),1e-5);
   >> regula(f,-7,-5,fzero(f,[-7 -5]),1e-5,eps,20);
   >> newton(f,df,-7,fzero(f,[-7 -5]),1e-5,eps,20);
   >> muller(f,-7,-6,-5,fzero(f,[-7 -5]),1e-5,eps,20);
   

   Plot of the function is given at the following figure;

   
   
   Then, the following tables are obtained.
   

   Table: Obtained root values at each iteration for all of four methods.

   iteration	Bisection	Regula	Newton	Muller
   1	-6.0000e+00	-5.5672e+00	-5.4650e+00	-5.7134e+00
   2	5.5000e+00	-5.7373e+00	-5.8008e+00	-5.7604e+00
   3	-5.7500e+00	-5.7575e+00	-5.7596e+00	-5.7591e+00
   4	-5.8750e+00	-5.7590e+00	-5.7591e+00	-5.7591e+00
   5	-5.8125e+00	-5.7591e+00	-5.7591e+00	-
   6	-5.7812e+00	-5.7591e+00	-	-

   
   
   

   Table: Obtained function values at each iteration for all of four methods.

   iteration	Bisection	Regula	Newton	Muller
   1	-4.4179e-01	3.1174e-01	4.5882e-01	7.8084e-02
   2	4.1006e-01	3.7524e-02	-7.3051e-02	-2.2184e-03
   3	1.5762e-02	2.8928e-03	-8.1042e-04	4.1882e-06
   4	-2.0681e-01	2.0926e-04	-1.0968e-07	-4.0674e-11
   5	-9.3753e-02	1.5061e-05	-2.2204e-15	-
   6	-3.8525e-02	1.0836e-06	-	-

   
   

   i

   Analyze these tables. Is the convergence sustained for the each methods? For the sustained ones; at which iteration and why?

   ii

   If the exact value is given as 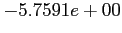$-5.7591e+00$, fill the following table for two methods. Choose two methods and use scientific notation with five significant figures.;
   
   

   iteration	$Error_1$	$Error_2$	$Error_3$	$Error_4$
   1	-2.4087e-01	1.9191e-01	2.9418e-01	4.5735e-02
   2	2.5913e-01	2.1820e-02	-4.1715e-02	-1.2812e-03
   3	9.1313e-03	1.6722e-03	-4.6817e-04	2.4198e-06
   4	-1.1587e-01	1.2090e-04	-6.3367e-08	-2.3500e-11
   5	-5.3369e-02	8.7017e-06	-1.7764e-15	-
   6	-2.2119e-02	6.2607e-07	-

   iteration	$Error Ratio_1$	$Error Ratio_2$	$Error Ratio_3$	$Error Ratio_4$
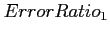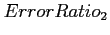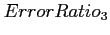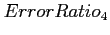   1	-2.4087e-01	1.9191e-01	2.9418e-01	4.5735e-02
   2	-1.0758e+00	1.1370e-01	-1.4180e-01	-2.8014e-02
   3	3.5238e-02	7.6636e-02	1.1223e-02	-1.8887e-03
   4	-1.2689e+01	7.2305e-02	1.3535e-04	-9.7116e-06
   5	4.6060e-01	7.1972e-02	2.8033e-08	-
   6	4.1445e-01	7.1948e-02	-	-

   iii

   What can you say about the speed of convergences for each method?

   iv

   Which method is the best one? Why?

2. Consider the same function with the previous question:

   v

   Find the root in the interval of $[-5,-3]$ with Newton's method. Hint: Newton's method uses the algorithm:
   

   $$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$$

   
   

   
   

   >> f = inline ( ' 3*sin( x) - exp ( x)/4 -1');
   >> df = inline ( ' 3*cos( x) - exp ( x)/4');
   >> fzero(f,[-5 -3])
   ans =  -3.484142626624529
   >> newton(f,df,-3,fzero(f,[-5 -3]),1e-5,eps,20);
      1.0000e+00  -3.4814e+00  -7.7103e-03   2.7199e-03   2.7199e-03
      2.0000e+00  -3.4841e+00  -3.7332e-06   1.3176e-06   4.8442e-04
      3.0000e+00  -3.4841e+00  -8.8107e-13   3.1086e-13   2.3594e-07
   >> fzero(f,[-7 -5])
   ans =  -5.943116471352441
   >> newton(f,df,-5,fzero(f,[-5 -3]),1e-5,eps,20);
      1.0000e+00  -7.2078e+00  -3.3953e+00  -3.7237e+00  -3.7237e+00
      2.0000e+00  -5.3280e+00   1.4480e+00  -1.8439e+00   4.9518e-01
      3.0000e+00  -6.1644e+00  -6.4514e-01  -2.6803e+00   1.4536e+00
      4.0000e+00  -5.9478e+00  -1.3352e-02  -2.4637e+00   9.1918e-01
      5.0000e+00  -5.9431e+00  -1.1028e-05  -2.4590e+00   9.9809e-01
      6.0000e+00  -5.9431e+00  -7.6171e-12  -2.4590e+00   1.0000e+00
   

   or

   ***********************************
   write the function
   function fx=func29i(x)
   fx= 3*sin( x) - exp ( x)/4 -1;
   save as func29i.m
   ***********************************
   write the function
   function fx=funcdiff29i(x)
   fx= 3*cos( x) - exp ( x)/4;
   save as funcdiff29i.m
   ***********************************
   

   start with
   

   $$x_0 = -3$$

   
   

   >> format long
   >> x0=-3;x1=x0-(func29i(x0)/funcdiff29i(x0))
   x1 =  -3.481422717761558
   >> x2=x1-(func29i(x1)/funcdiff29i(x1))
   x2 =  -3.484141309056956
   >> x3=x2-(func29i(x2)/funcdiff29i(x2))
   x3 =  -3.484142626624218
   >> x4=x3-(func29i(x3)/funcdiff29i(x3))
   x4 =  -3.484142626624529
   

   same procedure for $x_0 = -5$

   vi

   Estimate the error at the last iteration in your answer to part i. Hint: To estimate the error, compute one more iteration.
   

   >> x5=x4-(func29i(x4)/funcdiff29i(x4))
   x5 =  -3.484142626624529
   

   
   

   $$e_4 = x_5-x_4 = (-3.484142626624529) - (-3.484142626624529) = 0$$

   
   

   vii

   Approximately how many iterations of the bisection method would have been required to achieve the error value of $1e-5$?
   
   The error in the bisection method satisfies
   

   $$e_n=\vert\frac{Original Interval}{2^n} \vert$$

   
   

   $x_0 = -3$ In this case, taking the original interval to be [-5, -3], we would have
   

   $$e_n=\vert \frac{2}{2^n×} \vert$$

   
   

   Therefore, to achieve approximately the same error as we obtained with four iterations of Newton's method here, would require sufficient iterations of bisection to ensure
   

   $$\frac{2}{2^n}=1E-5$$

   
   

   this gives
   

   $$\frac{2}{0.00001}=e^{nln(2)}$$

   
   

   
   

   $$\frac{ln(\frac{2}{0.00001})}{ln(2)}=n$$

   
   

   
   

   $$n\cong 18$$

   
   

   >> format short
   >> bisect(f,-5,-3,fzero(f,[-5 -3]),1e-5);
   1.0000   -4.0000    0.5090   -0.3311   -0.3311
   2.0000   -3.5000   -0.3060    0.1689   -0.5100
   3.0000   -3.7500    0.1372   -0.0811   -0.4804
   4.0000   -3.6250   -0.0771    0.0439   -0.5409
   5.0000   -3.6875    0.0321   -0.0186   -0.4244
   6.0000   -3.6562   -0.0220    0.0126   -0.6780
   7.0000   -3.6719    0.0052   -0.0030   -0.2375
   8.0000   -3.6641   -0.0084    0.0048   -1.6056
   9.0000   -3.6680   -0.0016    0.0009    0.1886
   10.0000   -3.6699    0.0018   -0.0010   -1.1511
   11.0000   -3.6689    0.0001   -0.0001    0.0656
   12.0000   -3.6685   -0.0007    0.0004   -6.1168
   13.0000   -3.6687   -0.0003    0.0002    0.4183
   14.0000   -3.6688   -0.0001    0.0001    0.3046
   15.0000   -3.6689    0.0000   -0.0000   -0.1417
   16.0000   -3.6689   -0.0000    0.0000   -3.0289
   17.0000   -3.6689   -0.0000    0.0000    0.3349
   18.0000   -3.6689   -0.0000    0.0000    0.0071
   

   same result.

3. Consider this pair of equations:
   
   $$x^2+4y^2=4$$
   
   
   
   
   $$y-x^2+2x=0.5$$
   
   
   Plot of the system is given at the following figure;

   
   
   Solve this system by iteration. Hint: Start with something like $y=...$ and proceed only two iterations.
   

   >> fplot(@(x)[x^2-2*x+0.5,-sqrt(1-x^2/4),sqrt(1-x^2/4)],[-2 2 -1.2 1.2]);
       grid on;axis xy
   >> y=0.7;
   >> x=sqrt(4-4*y^2);yy=x^2-2*x+0.5;y=yy;D=[x,y];disp(D);
   1.4283   -0.3166   %xy-pair after first iteration
   >> x=sqrt(4-4*y^2);yy=x^2-2*x+0.5;y=yy;D=[x,y];disp(D);
   1.8971    0.3049   %xy-pair after second iteration
   >> x^2+4*y^2
   ans = 3.970877751497605 %should be equal to 4, see the pair of equations
   >> y-x^2+2*x
   ans = 0.500000000000000 %should be equal to 0.5, see the pair of equations
   

4. Consider the linear system;
   
   $$\begin{array}{r} x_1-2x_2+4x_3=6\\ 8x_1-3x_2+2x_3=2\\ -1x_1+10x_2+2x_3=4\\ \end{array}$$
   
   

   viii

   Solve this system by Gaussian elimination with pivoting. How many row interchanges are needed?

   ix

   What is the value of determinant?

   x

   Obtain the 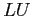$LU$ decomposition of the system.

   xi

   Repeat without any row interchanges (only for the first item). Do you get the same results? Why?

   >> A=[1 -2 4; 8 -3 2; -1 10 2]
   >> b=[6 2 4]
   >> GEPivShow(A,b')
   Begin forward elimination with Augmented system:
        1    -2     4     6
        8    -3     2     2
       -1    10     2     4
   Swap rows 1 and 2;  new pivot = 8
   After elimination in column 1 with pivot = 8.000000
       8.0000   -3.0000    2.0000    2.0000
            0   -1.6250    3.7500    5.7500
            0    9.6250    2.2500    4.2500
   Swap rows 2 and 3;  new pivot = 9.625
   After elimination in column 2 with pivot = 9.625000
       8.0000   -3.0000    2.0000    2.0000
            0    9.6250    2.2500    4.2500
            0         0    4.1299    6.4675
   ans =   -0.1132     0.0755     1.5660 %these are x1, x2, x3
   >> det(A)
   ans =   318
   >> 8.0000*9.6250 *4.1299 %product of the diagonal of U
   ans =  318.0023
   % For LU-decomposition
   >> [L,U,pv] = luPiv(A)
   L =    1.0000         0         0
           -0.1250    1.0000         0
            0.1250   -0.1688    1.0000
   U =   8.0000   -3.0000    2.0000
            0    9.6250    2.2500
            0         0    4.1299
   pv =
   
        2
        3
        1
   % two times pivoting
   % solution is completed
   %**********************************************
   % For proving purpose
   >> A=[1 -2 4; 8 -3 2; -1 10 2]
   A =
        1    -2     4
        8    -3     2
       -1    10     2
   % our Idendity matrix becomes for swaping rows 1 and 2
   >> pivoting1=[0 1 0; 1 0 0; 0 0 1]
   pivoting1 =
        0     1     0
        1     0     0
        0     0     1
   % apply this pivoting to our original matrix     
   >> A=pivoting1*A
   A =
        8    -3     2
        1    -2     4
       -1    10     2
   % our Idendity matrix becomes for swaping rows 2 and 3
   >> pivoting2=[1 0 0; 0 0 1; 0 1 0]
   pivoting2 =
        1     0     0
        0     0     1
        0     1     0
   
   % also apply this pivoting to our pivoted matrix     
   >> A=pivoting2*A
   A =
        8    -3     2
       -1    10     2
        1    -2     4
   >> [L,U,pv] = luPiv(A)
   L =
      1.000000000000000                   0                   0
     -0.125000000000000   1.000000000000000                   0
      0.125000000000000  -0.168831168831169   1.000000000000000
   U =
      8.000000000000000  -3.000000000000000   2.000000000000000
                      0   9.625000000000000   2.250000000000000
                      0                   0   4.129870129870130
   pv =
        1
        2
        3
   % it is proved.
   %**********************************************
   % for not pivoting case;
   >> GEshow(A,b')
   Begin forward elimination with Augmented system:
        1    -2     4     6
        8    -3     2     2
       -1    10     2     4
   After elimination in column 1 with pivot = 1.000000
        1    -2     4     6
        0    13   -30   -46
        0     8     6    10
   After elimination in column 2 with pivot = 13.000000
       1.0000   -2.0000    4.0000    6.0000
            0   13.0000  -30.0000  -46.0000
            0         0   24.4615   38.3077
   ans =    -0.1132     0.0755    1.5660
   >> 1.0000*13.0000*24.4615
   ans =   317.9995
   % Solutions are the same. They are same because the system is 
   % not ill-conditioned.