Ceng 375 Numerical Computing
Final Exam
Jan 18, 2011 11.30-14.00
Write your name and student ID to each paper. Answer all questions. Good Luck!
- (10pts) Choose only two questions. Each question is 5 points
- i
- Describe the general working of a bracketing method. What are the assumptions for this family of methods?
- ii
- Describe truncation and round-off errors. Give example.
- iii
- Why do we need pivoting while solving sets of equations by elimination methods? Can we skip pivoting and under which circumstances?
- iv
- What does singularity mean for a matrix? Make a comparison of singular and nonsingular matrices.
- v
- What are the differences between the interpolation and curve fitting?
- (5 pts) Derive the Newton's method formula using a Taylor series expansion.
- (25 pts)
For the given data points;
- (10 pts) Write out the Lagrangian polynomial from this table
- vi
- confirm that it reproduces the
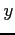 's for each
's for each 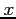 -value.
-value.
- vii
- interpolate with it to estimate
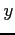 at
at  .
.
- viii
- extrapolate with it to estimate
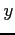 at
at  .
.
- (10 pts) Suppose in previous item that the
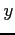 -value for
-value for 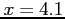 is mistakenly entered as
is mistakenly entered as 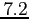 rather than
rather than 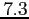 . Repeat the previous item with this incorrect value. How much difference does this make?
. Repeat the previous item with this incorrect value. How much difference does this make?
- (5 pts) Expand the Lagrangian polynomials in the previous items (a & b) to get the quadratics in the form
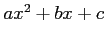 . How different are the values for
. How different are the values for 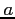 ,
, 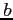 , and
, and 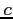 ?
?
- Choose only two questions.
- (20pts) Following system is given.
- ix
- (10 pts) Solve this system by Gaussian elimination with pivoting (use five significant digits of precision). How many row interchanges are needed?
- x
- (10 pts) You could have saved the row multipliers and obtained a
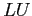 equivalent of the coefficient matrix. Use this
equivalent of the coefficient matrix. Use this 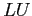 to solve with right-hand sides of
to solve with right-hand sides of ![$[-3,7,-2]^T$](img15.png)
- (20pts) Consider solving the following linear system by the Jacobi method.
- xi
- (5 pts) Write down the Jacobi iteration formula for this problem given initial guess
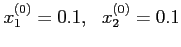 .
.
- xii
- (10 pts) Assume that the error vector at iteration
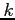 is denoted by
is denoted by 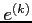 . How many iterations do we need before
. How many iterations do we need before
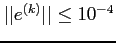 ?
?
- xiii
- (5 pts) Repeat with Gauss-Seidel method. Compare with Jacobi method.
- (20pts) Least Squares Method
- xiv
- (10 pts) A function
 is to be used as an approximation to a set of data
is to be used as an approximation to a set of data 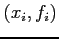 with
with
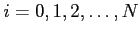 . Suppose further that the function
. Suppose further that the function  depends on two parameters
depends on two parameters 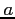 and
and 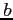 . Provide full details of how the parameters
. Provide full details of how the parameters 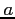 and
and 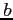 can be determined.
can be determined.
- xv
- (10 pts) Using the result of the previous item, obtain the normal equations for the function
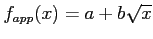 . Do not attempt to solve these equations.
. Do not attempt to solve these equations.
- Choose only two questions.
- (20pts) Write the expression to economize the the Maclaurin series for
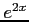 with the precision 0.08 by using Chebyshev polynomials. Do not perform the calculations.
with the precision 0.08 by using Chebyshev polynomials. Do not perform the calculations.
- (20pts) Fourier Series
- xvi
- (10 pts) Find the Fourier coefficients for
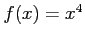 if it is periodic and one period extends from
if it is periodic and one period extends from 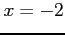 to
to  . Do not evaluate the integrals.
. Do not evaluate the integrals.
- xvii
- (10 pts) Write the Fourier series expansion for this function up to
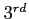 term.
term.
- (20pts) Consider the function
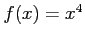 ;
;
- xviii
- (5 pts) Fill the following table within the five digit accuracy
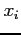 |
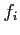 |
| 0.00000 |
0.00000 |
| |
|
| |
|
| |
|
| |
|
| |
|
| 1.20000 |
|
- xix
- (2.5 pts) Approximate
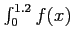 dx using the Composite Trapezoidal Rule and a step size of
dx using the Composite Trapezoidal Rule and a step size of 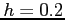 .
.
- xx
- (2.5 pts) Approximate
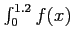 dx using the Composite Trapezoidal Rule and a step size of
dx using the Composite Trapezoidal Rule and a step size of 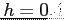 .
.
- xxi
- (10 pts) Estimate the error in your answers;
- Find the exact value of the integral simply by integrating the given function. Then, find the errors for parts ii and iii.
- Also use the global error formula to find the errors for parts ii and iii.
- Analyze and compare these error values.
Cem Ozdogan
2011-09-28
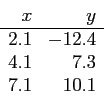
![\begin{displaymath}
\left[
\begin{array}{rrrr}
1 &-2 &4&6\\
8 &-3 &2&2\\
-1 &10 &2&4\\
\end{array} \right]
\end{displaymath}](img13.png)