Ceng 375 Numerical Computing
Midterm
Nov 10, 2010 14.40-16.30
Good Luck!
- (10 pts) A three digit, decimal machine which rounds all intermediate calculations, calculates the value of
What are the forward and backward errors error associated with this calculation?
- (10 pts) Derive the Newton's method formula using a Taylor series of
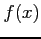 .
.
- (20 pts) Use Muller's method to find the root of
Figure 1:
Plot of the function, 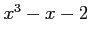 .
.
|
|
Start with  ,
, 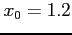 , and
, and 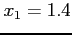 and find
and find 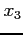 and
and 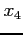 (two iterations).
(two iterations).
- (30 pts) Consider the function:
Figure 2:
Plot of the function, 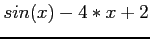 .
.
|
|
- i
- Use two iterations of Newton s method to estimate the root of this function between
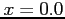 and
and 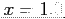 (Use four significant figures)
(Use four significant figures)
- ii
- Estimate the error in your answer to part i (Use more than four significant figures).
- iii
- Approximately how many iterations of the bisection method would have been required to achieve the same error of part ii? (Hint: if the value in part ii is negative, take absolute value of it.)
- (30 pts) Consider the linear system (
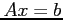 );
);
- iv
- Solve this system by Gaussian elimination with pivoting. How many row interchanges are needed?
- v
- What is the value of determinant?
- vi
- Obtain the
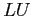 decomposition of the system.
decomposition of the system.
- vii
- Repeat without any row interchanges (only for the first item). Do you get the same results? Why?
Cem Ozdogan
2011-09-28
![\begin{displaymath}
A=\left[
\begin{array}{rrrr}
1 & 3 & 1 & 1 \\
2 & 5 & 2 &...
...egin{array}{r}
6 \\
2 \\
4 \\
3 \\
\end{array} \right]
\end{displaymath}](img17.png)