Ceng 375 Numerical Computing
Midterm
Nov 14, 2011 15.40-17.30
Good Luck!
- (30 pts) Consider the difference approximation for derivative of a function;
where 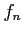 means
means 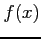 and
and 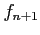 means
means 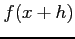
- i
- (15 pts) Use this formula to approximate the derivative of
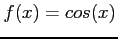 at
at  using step sizes of
using step sizes of 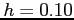 and
and 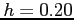 .
.
- ii
- (15 pts) Make an error analysis by finding the difference with the exact value at each step size,
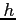 . Estimate the order of error
. Estimate the order of error 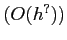 by the ratio of these errors.
by the ratio of these errors.
- (30 pts) Consider the solution to
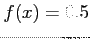 where
where 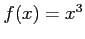 . Choosing initial guesses of
. Choosing initial guesses of 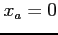 and
and 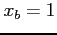 ,
,
- iii
- (5 pts) Describe the general working of a bracketing method. What are the assumptions for this family of methods? Are these assumptions satisfied for
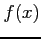 ?
?
- iv
- (10 pts) Write down an expression to show how the error
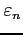 in the bisection method decreases with subsequent iterations. Find the required number of iterations when the error after
in the bisection method decreases with subsequent iterations. Find the required number of iterations when the error after 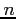 iterations is
iterations is 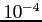
- v
- (15 pts) Using the bisection method, determine the solution to four decimal places by filling the table below. Does the number of iterations this took agree with the predicted number in previous item?
| i |
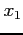 |
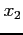 |
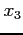 |
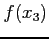 |
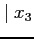 - -
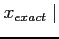 |
| 1 |
0.00000 |
1.00000 |
0.50000 |
0.12500 |
0.29370 |
| 2 |
0.50000 |
1.00000 |
0.75000 |
0.42188 |
0.04370 |
| 3 |
0.75000 |
1.00000 |
0.87500 |
0.66992 |
0.08130 |
| 4 |
0.75000 |
0.87500 |
0.81250 |
0.53638 |
0.01880 |
| 5 |
0.75000 |
0.81250 |
0.78125 |
0.47840 |
0.01245 |
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
- (25 pts) Consider the function
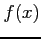 , on
, on ![$[0, 1]$](img25.png) , defined by
, defined by
- vi
- (10 pts) Describe how the secant method determine a smaller sub-interval containing a root.
- vii
- (15 pts) Apply the secant method to
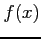 twice.
twice.
- (25 pts) Find the
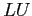 factorization of
factorization of
by Gaussian elimination (without pivoting). Clearly show how you get the entries of 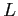 and
and 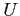 .
.
Cem Ozdogan
2012-01-17
![\begin{displaymath}
A=\left[
\begin{array}{rrrr}
1 & 3 & 1 & 1 \\
2 & 5 & 2 & 2 \\
-1 &-3 &-3 & 5 \\
1 & 3 & 2 & 2 \\
\end{array} \right]
\end{displaymath}](img28.png)