Next: About this document ...
![\includegraphics[width=3cm]{numerical/CankayaLogo_yeni}](img2.png) |
Çankaya University
Mcs 331 Numerical Methods Midterm Examination Dec 01, 2014 13.20 - 15.10 Good Luck! |
![\includegraphics[width=3cm]{numerical/DepartmentLogo_yeni}](img3.png) |
|
|
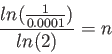
>> log(1/0.0001)/log(2) ans = 13.287712379549451
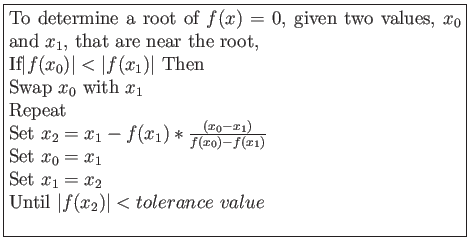
>> x0=1.0;
>> x1=0.0;
>> syms x;
fx='sqrt(x)-cos(x)';
>> subs(fx,x0)
ans = 0.45969769413186
>> subs(fx,x1)
ans = -1
>> x2=x1-subs(fx,x1)*((x0-x1)/(subs(fx,x0)-subs(fx,x1)))
x2 = 0.68507335732605
>> x0=x1
x0 = 0
>> x1=x2
x1 = 0.68507335732605
>> x2=x1-subs(fx,x1)*((x0-x1)/(subs(fx,x0)-subs(fx,x1)))
x2 = 0.65039498012836
>> solve('sqrt(x)-cos(x)')
ans = .64171437087288265839856530031652
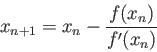
>> format long
>> x=-pi:0.1:pi
>> fzero('sin(x)-4*x+2',[0 1])
ans = 0.651618523135209
>> x=0;
>> sin(x)-4*x+2
ans = 2
>> x=1;
>> sin(x)-4*x+2
ans = -1.158529015192103
write the function
function fx=func(x)
fx=sin(x)-4*x+2;
save as func.m
write the function
function fx=funcdiff(x)
fx=cos(x)-4;
save as funcdiff.m
The best choice for >> x0=0;x0-(func(x0)/funcdiff(x0)) ans = 0.6667 (0.666666666666667) >> x0=0.6667;x0-(func(x0)/funcdiff(x0)) ans = 0.6516 (0.651640263601115) >> x0=0.6516;x0-(func(x0)/funcdiff(x0)) ans = 0.6516 (0.651618523167672)or start with
>> x0=1;x0-(func(x0)/funcdiff(x0)) ans = 0.6651 (0.665135766874333) >> x0=0.6651;x0-(func(x0)/funcdiff(x0)) ans = 0.6516 (0.651635876939131) >> x0=0.6516;x0-(func(x0)/funcdiff(x0)) ans = 0.6516 (0.651618523167672)Answer:
![\begin{displaymath}
A=\left[
\begin{array}{rrrr}
1 & 3 & 1 & 1 \\
2 & 5 & 2 &...
...egin{array}{r}
6 \\
2 \\
4 \\
3 \\
\end{array} \right]
\end{displaymath}](img29.png)
%**********************************************
%i) Ax=b
>> A=[1 3 1 1; 2 5 2 2; -1 -3 -3 5; 1 3 2 2]
>> b=[6 2 4 3]
>> format short
>> GEPivShow(A,b')
Begin forward elmination with Augmented system:
1 3 1 1 6
2 5 2 2 2
-1 -3 -3 5 4
1 3 2 2 3
Swap rows 1 and 2; new pivot = 2
After elimination in column 1 with pivot = 2.000000
2.0000 5.0000 2.0000 2.0000 2.0000
0 0.5000 0 0 5.0000
0 -0.5000 -2.0000 6.0000 5.0000
0 0.5000 1.0000 1.0000 2.0000
After elimination in column 2 with pivot = 0.500000
2.0000 5.0000 2.0000 2.0000 2.0000
0 0.5000 0 0 5.0000
0 0 -2.0000 6.0000 10.0000
0 0 1.0000 1.0000 -3.0000
After elimination in column 3 with pivot = -2.000000
2.0000 5.0000 2.0000 2.0000 2.0000
0 0.5000 0 0 5.0000
0 0 -2.0000 6.0000 10.0000
0 0 0 4.0000 2.0000
ans =
-21.0000
10.0000
-3.5000
0.5000
%**********************************************
% ii) Determinant
>> det(A)
ans = 8
>> 2.0000*0.5000*-2.0000*4.0000 %product of the diagonal of U
ans = 8
%**********************************************
% iii) For LU-decomposition
>> [L,U,pv]=luPiv(A)
L =
1.0000 0 0 0
0.5000 1.0000 0 0
-0.5000 -1.0000 1.0000 0
0.5000 1.0000 -0.5000 1.0000
U =
2.0000 5.0000 2.0000 2.0000
0 0.5000 0 0
0 0 -2.0000 6.0000
0 0 0 4.0000
pv =
2
1
3
4
% one time pivoting
%**********************************************
% iv) for not pivoting case;
>> GEshow(A,b')
Begin forward elmination with Augmented system:
1 3 1 1 6
2 5 2 2 2
-1 -3 -3 5 4
1 3 2 2 3
After elimination in column 1 with pivot = 1.000000
1 3 1 1 6
0 -1 0 0 -10
0 0 -2 6 10
0 0 1 1 -3
After elimination in column 2 with pivot = -1.000000
1 3 1 1 6
0 -1 0 0 -10
0 0 -2 6 10
0 0 1 1 -3
After elimination in column 3 with pivot = -2.000000
1 3 1 1 6
0 -1 0 0 -10
0 0 -2 6 10
0 0 0 4 2
ans =
-21.0000
10.0000
-3.5000
0.5000
% Solutions are the same. They are same because the system is
% not ill-conditioned.
% solution is completed
%**********************************************
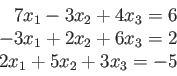
%**********************************************
%Switching rows 2 &3 first
>> A=[7 -3 4; 2 5 3; -3 2 6]
>> B=[6 -5 2]
>> jacobi(A,B',P',0.01,20)
k = 1 P =
0.857142857142857
-1.000000000000000
0.333333333333333
k = 2 P =
0.238095238095238
-1.542857142857143
1.095238095238095
k = 3 P =
-0.429931972789116
-1.752380952380953
0.966666666666667
k = 4 P =
-0.446258503401361
-1.408027210884354
0.702494331065760
k = 5 P =
-0.147722708130871
-1.242993197278911
0.579546485260771
k = 6 P =
-0.006737933268545
-1.288638807904114
0.673803045027535
k = 7 P =
-0.080161229117497
-1.401586653709102
0.759510636000432
k = 8 P =
-0.177543215018434
-1.423641889953260
0.760448270010952
k = 9 P =
-0.187531249986227
-1.385251675999198
0.719109022475203
k = 10 P =
-0.147455873985486
-1.356452913490631
0.701318267006619
k = 11 P =
-0.124947401214053
-1.361808610609777
0.711756367504134
k = 12 P =
-0.133207328835124
-1.377074860016859
0.724795836262899
k = 13 P =
-0.147201132157454
-1.381594570223690
0.725754622254725
k = 14 P =
-0.149686028527138
-1.376572320489853
0.720264290662503
k = 15 P =
-0.144396303445653
-1.372284162986646
0.717347759233048
k = 16 P =
-0.140891932270305
-1.372650134161568
0.718563235939389
k = 17 P =
-0.141743335177466
-1.374781168655511
0.720437411918703
k = 18 P =
-0.143727593377335
-1.375565113080236
0.720722055296438
k = 19 P =
-0.144226222918065
-1.374942195826928
0.719991241004744
>> gseid(A,B',P',0.001,20)
k = 1 P =
0.857142857142857
-1.342857142857143
1.209523809523809
k = 2 P =
-0.409523809523810
-1.561904761904762
0.649206349206349
k = 3 P =
-0.183219954648526
-1.316235827664399
0.680468631897203
k = 4 P =
-0.095797430083144
-1.369962207105064
0.742088687326783
k = 5 P =
-0.154034481517475
-1.383639419789080
0.717529232504289
k = 6 P =
-0.145862169912057
-1.372172671537751
0.717793138889889
k = 7 P =
-0.141098652881830
-1.374236422181201
0.720862814286152
k = 8 P =
-0.143737217669745
-1.375022801503793
0.719805658333059
k = 9 P =
-0.143470148263374
-1.374495335694486
0.719763371099808
% Gauss-Seidel iterates much faster