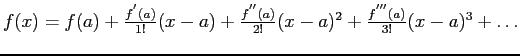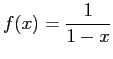Taylor Series
The expression for the order of error given above is found by comparison of the procedure with a Taylor series.
- A Taylor series is a power series that can approximate a function, f(x), for values near to x=a.
- Its coefficients use the derivatives of
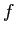 at
at 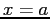
-
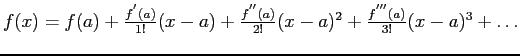
- The Taylor series says that if we know the values for all derivatives of
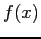 at
at 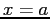 , we can approximate the function as closely as we desire.
, we can approximate the function as closely as we desire.
-
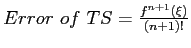 : The error term for a truncated Taylor series after the
: The error term for a truncated Taylor series after the 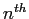 term
term
- where
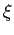 is a value between
is a value between 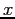 and
and 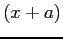 . Since the value of
. Since the value of 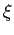 is not known, there is still uncertainty in the exact value of the error.
is not known, there is still uncertainty in the exact value of the error.
Example m-file: Taylor Series Approximations to 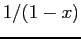 (http://siber.cankaya.edu.tr/ozdogan/NumericalComputations//mfiles/chapter0/demoTaylor.m demoTaylor.m)
(http://siber.cankaya.edu.tr/ozdogan/NumericalComputations//mfiles/chapter0/demoTaylor.m demoTaylor.m)
Consider the function
Make the Taylor series expansion of this function up to third order.
demoTaylor(1.6,0.8)
All of the Taylor polynomials agree with 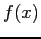 near
near 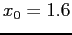 . The higher order polynomials agree over a larger range of
. The higher order polynomials agree over a larger range of 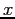 .
Cem Ozdogan
2011-12-27
.
Cem Ozdogan
2011-12-27