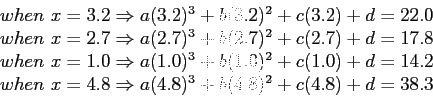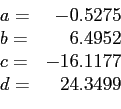Fitting a Polynomial to Data

• Interpolation involves constructing and then evaluating an interpolating function.
• interpolant, $y=F(x)$, determined by requiring that it pass through the known data $(x_i,y_i)$.
• In its most general form, interpolation involves determining the coefficients $a_1,a_2,\ldots,a_n$
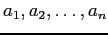
• in the linear combination of n basis functions, 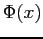$\Phi(x)$, that constitute the interpolant
  $$F(x)=a_1\Phi_1(x)+a_2\Phi_2(x)+\ldots+a_n\Phi_n(x)$$
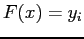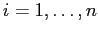  • such that $F(x)=y_i$ for $i=1,\ldots,n$. The basis function may be polynomial
    $$F(x)=a_1+a_2x+a_3x^2+\ldots+a_nx^{n-1}$$

  • or trigonometric
    $$F(x)=a_1+a_2e^{ix}+a_3e^{i2x}+\ldots+a_ne^{i(n-1)x}$$

  • or some other suitable set of functions.

• Polynomials are often used for interpolation because they are easy to evaluate and easy to manipulate analytically.
• Suppose that we have
  
  

  Table 5.1: Fitting a polynomial to data.

  x	f(x)
  3.2	22.0
  2.7	17.8
  1.0	14.2
  4.8	38.3
  5.6	51.7

  
  
• First, we need to select the points that determine our polynomial.
• The maximum degree of the polynomial is always one less than the number of points.

• Suppose we choose the first four points. If the cubic is $ax^3 + bx^2 + cx + d$,
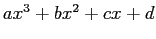• We can write four equations involving the unknown coefficients 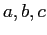$a, b, c$, and $d$;
  $$\begin{array}{r} when x = 3.2 \Rightarrow a(3.2)^3 + b(3.2... ...htarrow a(4.8)^3 + b(4.8)^2 + c(4.8) + d = 38.3 \\ \end{array}$$

• Solving these equations gives
  $$\begin{array}{lr} a=& -0.5275 \\ b=& 6.4952 \\ c=& -16.1177 \\ d= & 24.3499 \\ \end{array}$$

• and our polynomial is
  $$-0.5275x^3+6.4952x^2-16.1177x+24.3499$$

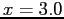• At $x=3.0$, the estimated value is 20.212.
• if we want a new polynomial that is also made to fit at the point $(5.6,51.7)$ ?
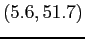• or if we want to see what difference it would make to use a quadratic instead of a cubic?
• Study this example in MATLAB; $Start \Rightarrow Toolboxes \Rightarrow CurveFitting \Rightarrow Curve  Fitting  Tool$.
  $» x=[ 3.2 2.7 1.0 4.8 5.6];$
  $» y=[22 17.8 14.2 38.3 51.7];$

• Another example;
  

  Table 5.2: Interpolation of gasoline prices.

  year	price
  1986	133.5
  1988	132.2
  1990	138.7
  1992	141.5
  1994	137.6
  1996	144.2

  
  
• Use the polynomial order 5, why?
  $$P=a_1+a_2y+a_3y^2+a_4y^3+a_5y^4+a_6y^5$$

• Make a guess about the prices of gasoline at year of 2011.

• Now, try with the shifted dates.
• Make the necessary corrections for the following lines $» years=year-mean(year);$
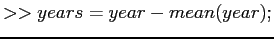
• What differs in the plot and why?
• Study this example in MATLAB; $Start \Rightarrow Toolboxes \Rightarrow CurveFitting \Rightarrow Curve  Fitting  Tool$.