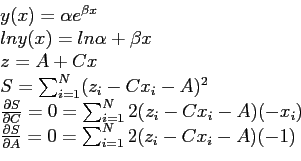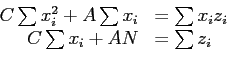- Fitting a cubic to the data by using MATLAB. For the given data points;
- Evaluate the cubic on the
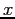 data and plot
data and plot
- Fitting a non-linear curve to the data with least-square method.
- Use the data in the previous item.
- We will fit
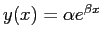 .
.
- Repeat each of the steps given in the following solution by hand.
Solution:
- First, we should compute a new table with
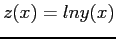
Then our new data points;
- Construct the normal equations (with
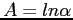 and
and 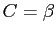 )
)
- Dividing each of these equations by
 and expanding the summation, we get the so-called normal equations
and expanding the summation, we get the so-called normal equations
- Solve these normal equations to find
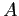 and
and 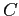
- So; we obtained
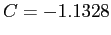 and
and 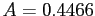 , we should convert back to the original variables. Convert back to the original variables
we have
, we should convert back to the original variables. Convert back to the original variables
we have
- Plot
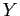 vs
vs 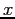 and
and 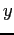 vs
vs 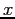 then compare them. For plotting (see Fig. 5.10);
then compare them. For plotting (see Fig. 5.10);
Figure 5.10:
plot(x,Y,'o',x,y,'-').
|
|
- Compare this least-square polynomial results with the built-in MATLAB functions results in the previous item (item 1), see Fig.5.11.
Figure 5.11:
plot(x,Y,'o',x,f,'-',x,y,'+').
|
|
Cem Ozdogan
2011-12-27