Differentiation with a Computer
- The derivative of a function,
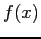 at
at 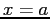 , is defined as
, is defined as
- This is called a forward-difference approximation.
- The limit could be approached from the opposite direction, giving a backward-difference approximation.
- Forward-difference approximation. A computer can calculate an approximation to the derivative, if a very small value is used for
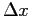 .
.
- Recalculating with smaller and smaller values of
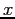 starting from an initial value.
starting from an initial value.
- What happens if the value is not small enough?
Table 7.1:
Forward-difference approximations for
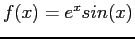 .
.
![\begin{table}\begin{center}
\includegraphics[scale=0.9,angle=0.5]{figures/5.1.ps}
\end{center}
\end{table}](img1075.png) |
With MATLAB. Analytical answer to the function of Table 7.1.
With MATLAB. Numerical answer to the function of Table 7.1.
- The two error terms of Eqs. 7.1 and 7.2 are not identical though both are
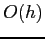 .
.
- If we add Eqs. 7.1 and 7.2, then divide by 2, we get the central-difference approximation to the derivative:
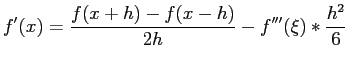 |
(7.3) |
- We had to extend the two Taylor series by an additional term to get the error because the
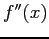 terms cancel.
terms cancel.
- This shows that using a central-difference approximation is a much preferred way to estimate the derivative.
- Even though we use the same number of computations of the function at each step,
- we approach the answer much more rapidly.
With MATLAB,
Table 7.2 illustrates this, showing that errors decrease about four fold when 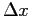 is halved (as Eq. 7.3 predicts) and that a more accurate value is obtained.
is halved (as Eq. 7.3 predicts) and that a more accurate value is obtained.
Table 7.2:
Central-difference approximations for
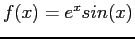 .
.
![\begin{table}\begin{center}
\includegraphics[scale=1]{figures/5.2.ps}
\end{center}
\end{table}](img1092.png) |
Cem Ozdogan
2011-12-27
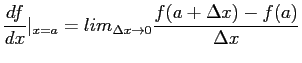
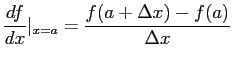
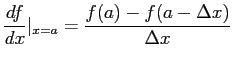
![]() is halved (as Eq. 7.3 predicts) and that a more accurate value is obtained.
is halved (as Eq. 7.3 predicts) and that a more accurate value is obtained.