Ceng 375 Numerical Computing
Final
Aug 8, 2005 09.00-11.00
Good Luck!
1 (20 Pts)
- i
- A three digit, decimal machine which rounds all intermediate calculations, calculates the value of
What are the forward
error associated with this calculation?
2 (20 Pts) In Newton's method the approximation 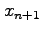 to a root of
to a root of 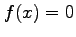 is computed from the approximation
is computed from the approximation 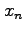 using the equation
using the equation
- ii
- Derive the above formula, using a Taylor series of
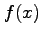 .
.
- iii
- For
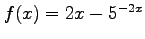 , refine the approximation
, refine the approximation 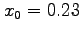 to the unique root of
to the unique root of 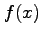 by carrying out one iteration of Newton's method.
by carrying out one iteration of Newton's method.
- iv
- What are the assumptions under which the above formula for Newton's method work?
3 (25 Pts) Consider the matrix
- v
- Use the Gaussian elimination method to triangularize this matrix and from that gets its determinant.
- vi
- Get the inverse of the matrix through Gaussian elimination.
- vii
- Get the inverse of the matrix through Gauss-Jordan method.
4 (25 Pts)
- viii
- Find the Fourier coefficients for
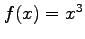 if it is periodic and one period extends from
if it is periodic and one period extends from 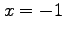 to
to 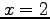 . Do not evaluate the integrals.
. Do not evaluate the integrals.
- ix
- Write the Fourier series expansion for this function up to
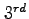 term.
term.
5 (20 Pts) Consider the difference approximation
where 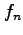 means
means 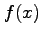 and
and 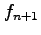 means
means 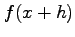
- x
- Use this formula to approximate the derivative of
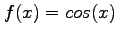 at
at 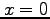 using step sizes of
using step sizes of 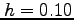 and
and 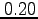 .
.
- xi
- Make an error analysis. Estimate the order of error
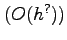 .
.
Hints: The ratio of errors and the difference with the exact value.
2006-09-28
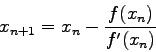
![\begin{displaymath}
A=\left[
\begin{array}{rrr}
3 &-1 &2\\
1 & 1 &3\\
-3 & 0 &5\\
\end{array} \right]
\end{displaymath}](img9.png)