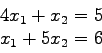Ceng 375 Numerical Computing
Midterm
July 18, 2005 09.00-11.00
Good Luck!
1 (20 Pts) Consider the function:
- i
- Show that this function has a simple root in the interval
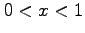
- ii
- Estimate this root using two iterations of the Secant Method.
- iii
- Estimate the error in your answer to part ii.
2 (25 Pts)Consider the function:
- iv
- Use two iterations of Newton s method to estimate the root of this function between
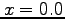 and
and 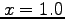
- v
- Estimate the error in your answer to part i.
- vi
- Approximately how many iterations of the bisection method would have been required to achieve the same error?
3 (30 Pts) Solve this system by Gaussian elimination with pivoting
- vii
- How many row interchanges are needed?
- viii
- Repeat without any row interchanges. Do you get the same results?
- ix
- You could have saved the row multipliers and obtained a
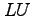 equivalent of the coefficient matrix. Use this
equivalent of the coefficient matrix. Use this 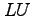 to solve but with right-hand sides of
to solve but with right-hand sides of ![$[1,-3,5]^T$](img8.png)
4 (25 Pts) Consider solving the following linear system by the Jacobi method.
- x
- Write down the Jacobi iteration formula for this problem given initial guess
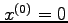 .
.
- xi
- Assume that the error (vector) at iteration
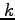 is denoted by
is denoted by 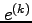 and that
and that 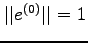 . How many iterations do we need before
. How many iterations do we need before
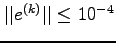 ?
?
2006-09-28
![\begin{displaymath}
\left[
\begin{array}{rrrr}
1 &-2 &4&6\\
8 &-3 &2&2\\
-1 &10 &2&4\\
\end{array} \right]
\end{displaymath}](img6.png)