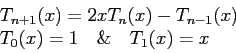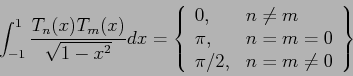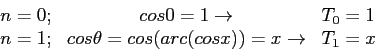Chebyshev Polynomials
Figure 1:
Plot of the first four polynomials of the Chebyshev polynomials.
|
|
- The members of this series of polynomials can be generated from the two-term recursion formula
- They form an orthogonal set,
- The Chebyshev polynomials are also terms of a Fourier series, because
where
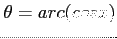 . Observe that
. Observe that
- Because of the relation
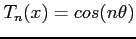 , the Chebyshev polynomials will have a succession of maxima and minima of alternating signs, as Figure 1 shows.
, the Chebyshev polynomials will have a succession of maxima and minima of alternating signs, as Figure 1 shows.
- MATLAB has no commands for these polynomials but this M-file will compute them:
if symop does not exist, http://siber.cankaya.edu.tr/ozdogan/NumericalComputations/mfiles/chapter4/symop.m download.
- All polynomials of degree
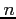 that have a coefficient of one on
that have a coefficient of one on 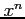 , the polynomial
, the polynomial
has a smaller upper bound to its magnitude in the interval [-1, 1].
- This is important because we will be able to write power function approximations to functions whose maximum errors are given in terms of this upper bound.
- Example m-file: Comparison of Lagrangian interpolation polynomials for equidistant and non-equidistant (Chebyshev) sample points for the function
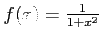 (http://siber.cankaya.edu.tr/ozdogan/NumericalComputations/mfiles/chapter4/lagrange_chebyshev.mlagrange_chebyshev.m )
(http://siber.cankaya.edu.tr/ozdogan/NumericalComputations/mfiles/chapter4/lagrange_chebyshev.mlagrange_chebyshev.m )
Cem Ozdogan
2010-12-19