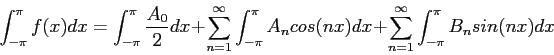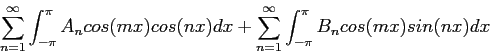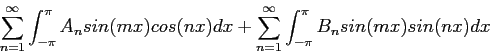- Polynomials are not the only functions that can be used to approximate the known function.
- Another means for representing known functions are approximations that use sines and cosines, called Fourier series.
- Any function can be represented by an infinite sum of sine and cosine terms with the proper coefficients, (possibly with an infinite number of terms).
- Any function,
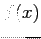 , is periodic of period
, is periodic of period 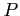 if it has the same value for any two x-values, that differ by
if it has the same value for any two x-values, that differ by 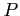 , or
, or
Figure 1:
Plot of a periodic function of period P.
|
|
Figure 1 shows such a periodic function. Observe that the period can be started at any point on the 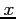 -axis.
-axis.
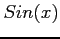 and
and 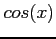 are periodic of period
are periodic of period 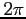
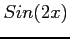 and
and 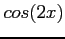 are periodic of period
are periodic of period 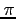
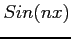 and
and 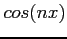 are periodic of period
are periodic of period 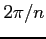
- We now discuss how to find the
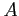 s and
s and 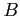 s in a Fourier series of the form
s in a Fourier series of the form
![\begin{displaymath}
f(x)\approx \frac{A_0}{2}+ \sum_{n=1}^{\infty} [A_ncos(nx)+B_nsin(nx)]
\end{displaymath}](img22.png) |
(1) |
The determination of the coefficients of a Fourier series (when a given function,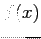 , can be so represented) is based on the property of orthogonality for sines and cosines. For integer values of
, can be so represented) is based on the property of orthogonality for sines and cosines. For integer values of 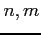 :
:
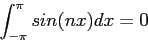 |
(2) |
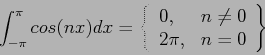 |
(3) |
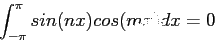 |
(4) |
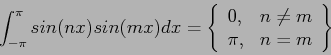 |
(5) |
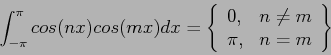 |
(6) |
It is related to the same term used for orthogonal (perpendicular) vectors whose dot product is zero. Many
functions, besides sines and cosines, are orthogonal (such as the Chebyshev polynomials).
- To begin, we assume that
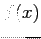 is periodic of period
is periodic of period 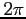 and can be represented as in Eq. 1. We find the values of
and can be represented as in Eq. 1. We find the values of 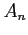 and
and 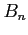 in Eq. 1 in the following way;
in Eq. 1 in the following way;
- For
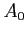 ; multiply both sides of Eq. 1 by
; multiply both sides of Eq. 1 by 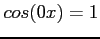 , and integrate term by term between the limits of
, and integrate term by term between the limits of 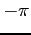 and
and 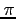 .
.
Because of Eqs. 2 and 3, every term on the right vanishes except the first, giving
Hence, 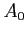 is found and it is equal to twice the average value of
is found and it is equal to twice the average value of 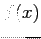 over one period.
over one period.
- For
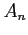 ; multiply both sides of Eq. 1 by
; multiply both sides of Eq. 1 by 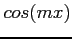 , where
, where 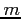 is any positive integer, and integrate:
is any positive integer, and integrate:
Because of Eqs. 3,4 and 6 the only nonzero term on the right is when  in the first summation, so we get a formula for the
in the first summation, so we get a formula for the 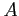 s;
s;
- For
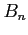 ; multiply both sides of Eq. 1 by
; multiply both sides of Eq. 1 by 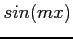 , where
, where 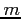 is any positive integer, and integrate:
is any positive integer, and integrate:
Because of Eqs. 2, 4 and 5, the only nonzero term on the right is when  in the second summation, so we get a formula for the
in the second summation, so we get a formula for the  s;
s;
It is obvious that getting the coefficients of Fourier series involves many integrations.
Subsections
Cem Ozdogan
2010-12-29