Next: About this document ... Up: Nonlinear Systems Previous: Nonlinear Systems
| y-value | x-value |
| 2 | 0.69315 |
| 2.88539 | 1.05966 |
| 2.72294 | 1.00171 |
| 2.71829 | 1.00000 |
| 2.71828 | 1.00000 |
![]() Example: Another example for the pair of equations whose plot is Fig. 7.
Example: Another example for the pair of equations whose plot is Fig. 7.
equations;
rearrangement;
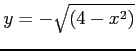 , , |
and begin with ![]() , the successive values for y and x are: (See Table 4)
, the successive values for y and x are: (See Table 4)
| y-value | x-value |
| -1.7291 | 1.0051 |
| -1.72975 | 1.00398 |
| -1.72961 | 1.00421 |
| -1.72964 | 1.00416 |
| -1.72963 | 1.00417 |
![]() We are converging to the solution in an oscillatory manner.
We are converging to the solution in an oscillatory manner.
Cem Ozdogan 2010-10-13