- The wait-for graph scheme is not applicable to a resource-allocation system with multiple instances of each resource type.
- We turn now to a deadlock-detection algorithm that is applicable to such a system. The algorithm employs several time-varying data structures:
- Available. A vector of length
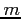 indicates the number of available resources of each type.
indicates the number of available resources of each type.
- Allocation. An
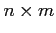 matrix defines the number of resources of each type currently allocated to each process.
matrix defines the number of resources of each type currently allocated to each process.
- Request. An
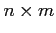 matrix indicates the current request of each process.
matrix indicates the current request of each process.
- If
![$Request[i][j]$](img71.png) equals
equals 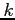 , then process
, then process 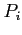 is requesting
is requesting 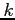 more instances of resource type
more instances of resource type 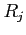 .
.
- The detection. algorithm described here simply investigates every possible allocation sequence for the processes that remain to be completed.
- Let
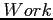 and
and 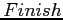 be vectors of length
be vectors of length 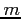 and
and 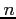 , respectively. Initialize
, respectively. Initialize
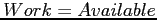 . For
. For
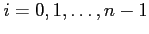 , if
, if
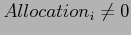 , then
, then
![$Finish[i]=false$](img79.png) ; otherwise,
; otherwise,
![$Finish[i]=true$](img80.png) .
.
- Find an index
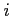 such that both
such that both
- a.
-
![$Finish[i]==false$](img82.png)
- b.
-
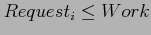
If no such 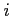 exists, go to step 4.
exists, go to step 4.
-
![$Finish[i]=true$](img80.png)
Go to step 2.
- If
![$Finish[i]==false$](img82.png) , for some
, for some
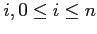 , then the system is in a deadlocked state. Moreover, if
, then the system is in a deadlocked state. Moreover, if
![$Finish[i]==false$](img82.png) , then process
, then process 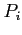 is deadlocked.
is deadlocked.
- Consider a system with five processes
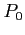 through
through 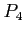 and three resource types
and three resource types 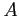 ,
, 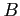 , and
, and 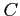 .
.
- Resource type
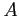 has seven instances,
has seven instances,
- Resource type
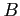 has two instances,
has two instances,
- Resource type
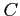 has six instances.
has six instances.
- Suppose that, at time
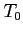 , we have the following resource-allocation state:
, we have the following resource-allocation state:
| |
Allocation |
Request |
Available |
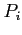 |
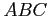 |
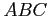 |
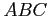 |
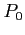 |
010 |
000 |
000 |
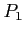 |
200 |
202 |
|
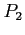 |
303 |
000 |
|
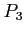 |
211 |
100 |
|
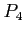 |
002 |
002 |
|
- If the algorithm is executed, it will be found that the sequence
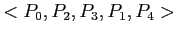 results in
results in
![$Finish[i] == true$](img89.png) for all
for all 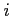 .
.
- Suppose now that process
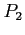 makes one additional request for an instance of type
makes one additional request for an instance of type 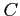 .
.
- Although we can reclaim the resources held by process
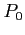 , the number of available resources is not sufficient to fulfill the requests of the other processes. Thus, a deadlock exists, consisting of processes
, the number of available resources is not sufficient to fulfill the requests of the other processes. Thus, a deadlock exists, consisting of processes 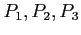 , and
, and 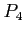 .
.
Cem Ozdogan
2010-04-19