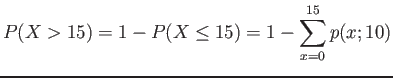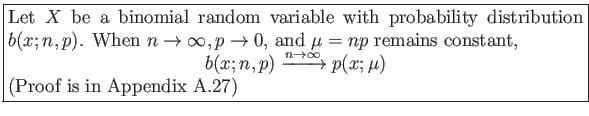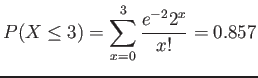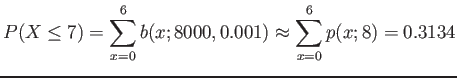- Poisson experiments: Experiments yielding numerical values of a random variable
 , the number of outcomes occurring during a given time interval or in a specified region.
, the number of outcomes occurring during a given time interval or in a specified region.
- Examples:
- the number of telephone calls per hour received by an office
- the number of postponed baseball games due to rain
- the number of field mice per acre
- the number of typing error per page
- The examples of the random variables that are having Poisson probability distribution are usually rare events such as # of car accident, # of flood or hurricane occurrences.
- So the Poisson distribution provides the fundamental idea of the Law of Small Numbers (LSN).
- Properties of Poisson Process:
- The number of outcomes in one time interval or specified region is independent of the number that occurs in any other disjoint time interval or region of space. In this way we say that the Poisson process has no memory.
- The probability that a single outcome will occur during a very short time interval or in a small region is proportional to the
length of the time interval or the size of the region and does not depend on the number of outcomes occurring outside this time interval or region.
- The probability that more than one outcome will occur in such a short time interval or fall in such a small region is negligible.
- Poisson Distribution: The probability distribution of the Poisson random variable
 , representing the number of outcomes occurring in a given time interval or specified region denoted by
, representing the number of outcomes occurring in a given time interval or specified region denoted by  , is (mean number
, is (mean number
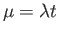 )
)
- where
 is the average number of outcomes per unit time or region, and
is the average number of outcomes per unit time or region, and 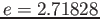 .
.
- Example 5.20: During a laboratory experiment the average number of radioactive particles passing through a counter in 1
millisecond is 4.
- What is the probability that 6 particles enter the counter in a given millisecond? (see Table A.2)
Figure:
Poisson Probability Sums
 .
.
|
|
- Example 5.21: Ten is the average number of oil tankers arriving each day at a certain port city.
- The facilities at the port can handle at most 15 tankers per day.
- What is the probability that on a given day tankers have to be turned away?
- Theorem 5.5:

- Example: In Example 5.20,
 .
.
- Using Chebyshev's theorem, we conclude that at least 3/4 of the time the number of radioactive particles entering the counter will be anywhere from 0 to 8 during a given millisecond.
- The Poisson Distribution As a Limiting Form of the Binomial: Theorem 5.6:
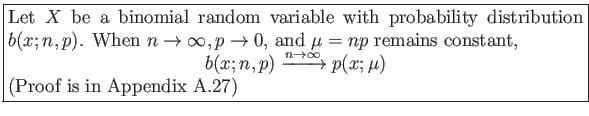
- If
 , we can change
, we can change  to a value close to 0 by interchanging what we have defined to be a success and a failure.
to a value close to 0 by interchanging what we have defined to be a success and a failure.
Figure 5.4:
Poisson density functions for different means.
|
|
The shape becomes more symmetric as the mean grows large.
- Example 5.22: The probability of an accident in a certain industrial facility on any given day is 0.005 and accidents are independent of each other.
- xvii
- What is the probability that in any given period of 400 days there will be an accident on one day?
- xviii
- What is the probability that there are at most three days with an accident?
- Example 5.23: In a manufacturing process where glass products are produced, defects or bubbles occur, occasionally
rendering the piece undesirable for marketing.
- It is known that, on average, 1 in every 1000 of these items produced has one or more bubbles.
- What is the probability that a random sample of 8000 will yield fewer than 7 items processing bubbles?
- Solution:
Cem Ozdogan
2012-02-15