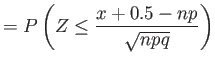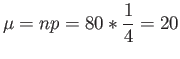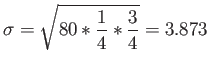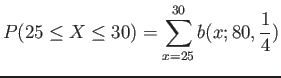- Poisson distribution can be used to approximate binomial probabilities when
 is quite large and
is quite large and  is very close to 0 or 1.
is very close to 0 or 1.
- Normal distribution not only provide a very accurate approximation to binomial distribution when
 is large and
is large and  is not extremely close to 0 or 1,
is not extremely close to 0 or 1,
- But also provides a fairly good approximation even when
 is small and
is small and  is reasonably close to
is reasonably close to
 .
.
Figure 6.20:
Normal approximation of
 .
.
|
|
- Theorem 6.2:

-
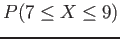
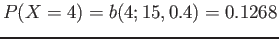
Figure 6.21:
Normal approximation of
 and
and
 .
.
|
|
- The degree of accuracy, which depends on how well the curve fits the histogram, will increase as n increases.
- If both
 and
and  are greater than or equal to 5, the normal approximation will be good.
are greater than or equal to 5, the normal approximation will be good.
Figure 6.22:
Histogram for
 .
.
|
|
Figure 6.23:
Histogram for
 .
.
|
|
- Let
 be a binomial random variable with parameters
be a binomial random variable with parameters  and
and  .
.
- Then
 has approximately a normal distribution with mean
has approximately a normal distribution with mean 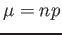 and variance
and variance
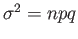 and
and
and the approximation will be good if  and
and  are greater than or equal to 5.
are greater than or equal to 5.
- Example 6.15: The probability that a patient recovers from a rare blood disease is 0.4.
- If 100 people are known to have contracted this disease, what is the probability that less than 30 survive?
- Solution:
Figure 6.24:
Area for Example 6.15.
|
|
- Example 6.16: A multiple-choice quiz has 200 questions each with 4 possible answers of which only 1 is correct answer.
- What is the probability that sheer guess-work yields from 25 to 30 correct answers for 80 of the 200 problems about which the student has no knowledge?
- Solution:
Figure 6.25:
Area for Example 6.16.
|
|
Cem Ozdogan
2012-02-15


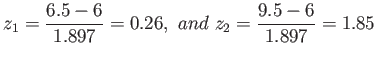
![]()