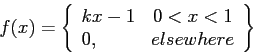Ceng 272 Statistical Computations
Final
June 04, 2010 11:00 - 13:00
Good Luck!
You are allowed to use CALCULATOR.
No any other electronic equipment is allowed.
Write the solutions explicitly and use the statistical terminology
Answer all the questions.
- (10 pts)
- i
- Dice roll:
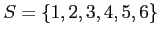 . Two events
. Two events
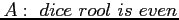 and
and
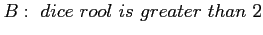 .
.
- a)
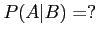
- b)
- Are these two events (
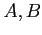 ) independent?
) independent?
- ii
- An electrical engineering lab has 20 probes of which 3 are bad. A student selects 2 probes randomly, what is the probability that both are bad?
- (15 pts) Consider the density function
- iii
- Evaluate
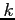
- iv
- Find
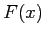 and use it to evaluate
and use it to evaluate
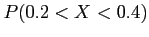
- (10 pts) The random variable
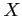 , representing the number of errors per 100 lines of software code, has the following probability distribution:
, representing the number of errors per 100 lines of software code, has the following probability distribution:
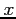 |
2 |
3 |
4 |
5 |
6 |
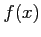 |
0.01 |
0.25 |
0.4 |
0.3 |
0.04 |
Find the expected value and the variance of 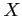 .
.
- (15 pts) A foreign student club lists as its members 3 Canadians, 4 Japanese, 6 Italians, and 3 Germans. If a committee of 4 is selected at random, find the probability that
- v
- all nationalities are represented;
- vi
- all nationalities except the Italians are represented.
- (15 pts) The average life of a certain type of small motor is 12 years with a standard deviation of 3 years. The manufacturer replaces free all motors that fail while under guarantee. If he is willing to replace only 6% of the motors that fail, how long a guarantee should he offer? Assume that the lifetime of a motor follows a normal distribution.
- (15 pts) Evaluate
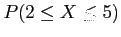 for a binomial variable with n = 12 and p = 0.2 by using
for a binomial variable with n = 12 and p = 0.2 by using
- vii
- From corresponding Table.
- viii
- From normal-curve approximation.
- (15 pts) In a certain city, the daily consumption of water (in millions of liters) follows approximately a gamma distribution with
 and
and 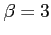 . If the daily capacity of that city is 9 million liters of water, what is the probability that on any given day the water supply is inadequate?
. If the daily capacity of that city is 9 million liters of water, what is the probability that on any given day the water supply is inadequate?
- (15 pts) The heights of 1000 students are approximately normally distributed with a mean of 174.5 centimetres and a standard deviation of 6.9 centimetres. If 200 random samples of size 25 are drawn from this population and the means recorded to the nearest tenth of a centimetre, determine
- ix
- the mean and standard deviation of the sampling distribution of
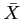 ;
;
- x
- the number of sample means that fall between 172.5 and 175.8 centimetres inclusive;
- xi
- the number of sample means falling below 172.0 centimetres.
Cem Ozdogan
2010-06-03