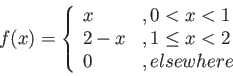Ceng 272 Statistical Computations
Midterm
Apr 04, 2012 17:40 - 19:20
Good Luck!
Answer all the questions.
Write the solutions explicitly and use the statistical terminology.
Calculator is allowed.
You are not allowed to use any other electronic equipment in the exam.
- (10 pts) An important property of a fiber is its water absorbency. A random sample of 20 pieces of cotton fiber is taken and the absorbency on each piece was measured. The following are the absorbency values
| 18.71 |
21.41 |
20.72 |
21.81 |
19.29 |
22.43 |
20.17 |
| 23.71 |
19.44 |
20.50 |
18.92 |
20.33 |
23.00 |
22.85 |
| 19.25 |
21.77 |
22.11 |
19.77 |
18.04 |
21.12 |
|
- i
- Calculate the sample mean and median for the above sample values.
- ii
- Compute the 10% trimmed mean.
- iii
- Compute the sample variance.
- iv
- Compute the standard deviation.
- (10 pts) Drawing names out of a hat for a lottery. Don't put names back in if they get drawn. Suppose we have 60 students and we draw 3 names.
- (i)
- How many possible outcomes if we keep track of the order of names?
- (ii)
- How many set of 3 names are possible if the order they are drawn is ignored?
- (20 pts) You are building a computer from components. You can buy the mainboard from 2 companies (A,B), RAM from 4 companies (A,C,D,E), hard drive from 3 companies (B,D,F) and graphics card from 2 companies (G,H). For each component, you are equally likely to buy from any one of the companies manufacturing that component.
- (i)
- Draw the tree diagram. What is the number of points in sample space?
- (ii)
- What is the probability of the event
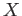 , P(X), that you build a computer that has at least one part from company D?
, P(X), that you build a computer that has at least one part from company D?
- (iii)
- What is the probability of the event
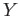 , P(Y), that RAM chip from company D?
, P(Y), that RAM chip from company D?
- (iv)
- What is the probability of the event
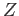 , P(Z), that HD from company D?
, P(Z), that HD from company D?
- (v)
- Notice that
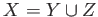 . Then
. Then
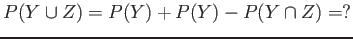
- (10 pts) 100 patients in a certain hospital were randomly selected and asked if they smoke (
 ) or not (
) or not ( ) and whether they have chronic bronchitis (
) and whether they have chronic bronchitis (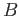 ) or not (
) or not (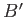 ). Based on this information
). Based on this information
| |
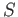 |
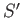 |
Row total |
Having bronchitis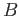 |
50 |
10 |
60 |
Not having bronchitis 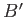 |
20 |
20 |
40 |
| Marginal total (column) |
70 |
30 |
100 |
- (a)
- If one patient is selected at random from these patients, find the probability that this patient is
- v
- P(non-smoker)
- vi
- P(smoker who has chronic bronchitis)
- vii
- P(smoker given that the patient has chronic bronchitis)
- viii
- P(non-smoker given that the patient does not have bronchitis)
- (b)
- Are two events
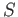 ,
, 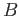 independent?
independent?
- (15 pts) A regional telephone company operates three identical relay stations at different locations. During a one year period, the number of malfunctions reported by each station and the causes are shown below.
| Station |
A |
B |
C |
| Problems with electricity supplied |
2 |
1 |
1 |
| Computer malfunction |
4 |
3 |
2 |
| Malfunctioning electrical equipment |
5 |
4 |
2 |
| Caused by other human errors |
7 |
7 |
5 |
Suppose that a malfunction was reported and it was found to be ``caused by other human errors''. What is the probability that it came from station C?
- (20 pts) The total number of hours, measured in units of 100 hours, that a family runs a vacuum cleaner over a period of one year is a random variable
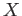 that has the density function
that has the density function
Find the probability that over a period of one year, a family runs their vacuum cleaner
- ix
- less than 120 hours;
- x
- between 50 and 100 hours.
- (20 pts) Let
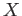 denote the number of times a certain numerical control machine will malfunction: 1, 2, or 3 times on any given day. Let
denote the number of times a certain numerical control machine will malfunction: 1, 2, or 3 times on any given day. Let 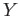 denote the number of times a technician is called on an emergency call. Their
joint probability distribution is given as
denote the number of times a technician is called on an emergency call. Their
joint probability distribution is given as
| |
|
|
x |
|
| f(x,y) |
|
1 |
2 |
3 |
| |
1 |
0.05 |
0.05 |
0.1 |
| y |
2 |
0.05 |
0.1 |
0.35 |
| |
3 |
0 |
0.2 |
0.1 |
- xi
- Evaluate the marginal distribution of
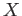 ;
;
- xii
- Evaluate the marginal distribution of
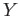 ;
;
- xiii
- Find
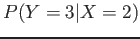 .
.
Cem Ozdogan
2012-04-16