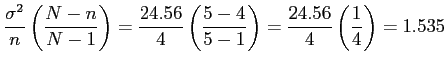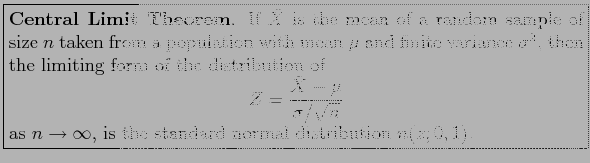- Suppose that a random sample of
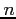 observations is taken from a normal population with mean
observations is taken from a normal population with mean 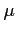 and variance
and variance 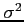 .
.
- By the reproductive property of the normal distribution (established in Theorem 7.11)
The standard deviation of the sample mean,
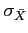 is called the standard error of
is called the standard error of 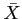 .
.
- We call
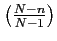 the finite population correction and it approaches 1 as
the finite population correction and it approaches 1 as
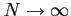 .
.
- Example: The following data gives the years of employment for all five employees (
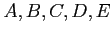 ) at the University Medical Center: 7, 8, 12, 7, 20.
) at the University Medical Center: 7, 8, 12, 7, 20.
- Let
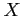 denote the number of years of employment. The population distribution (
denote the number of years of employment. The population distribution (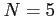 ) of
) of 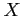 will be
will be
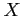 |
7 |
8 |
12 |
20 |
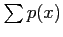 |
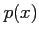 |
2/5 |
1/5 |
1/5 |
1/5 |
1.0 |
- Population mean;
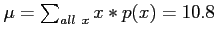 years
years
- Population variance;
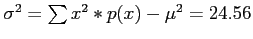
- Now, we take a sample of size
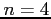 .
.
- There will be
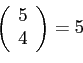 ways of making combinations.
ways of making combinations.
- The following table shows the list all the possible samples (without replacement) that can be selected from this population.
| Sample No |
Sample |
Sample Mean 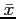 |
| 1 |
(A,B,C,D) = 7,8,12,7 |
8.5 |
| 2 |
(A,B,C,E) = 7,8,12,20 |
11.75 |
| 3 |
(A,B,D,E) = 7,8,7,20 |
10.5 |
| 4 |
(A,C,D,E) = 7,12,7,20 |
11.5 |
| 5 |
(B,C,D,E) = 8,12,7,20 |
11.75 |
- Calculate the sample mean for each of these samples. Then, the sampling distribution of
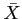 is
is
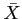 |
8.5 |
10.5 |
11.5 |
11.75 |
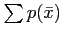 |
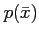 |
1/5 |
1/5 |
1/5 |
2/5 |
1.0 |
- Theorem 8.2:
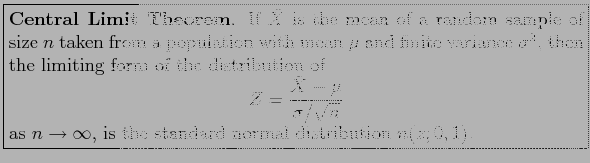
- The normal approximation for
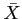 will generally be good if
will generally be good if
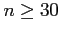 .
.
- If
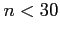 , the approximation is good only if the population is not too different from a normal distribution.
, the approximation is good only if the population is not too different from a normal distribution.
- This is true no matter what the population distribution may be as long as the population has a finite variance
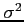 .
.
- This marvellous and famous fact in probability theory is called the Central Limit Theorem.
- This is remarkable and an universal probability law.
- If the population is known to be normal, the sampling distribution of
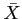 will follow a normal distribution exactly, no matter how small the size of the samples.
will follow a normal distribution exactly, no matter how small the size of the samples.
Figure:
Illustration of the central limit theorem (distribution of 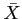 for
for 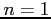 , moderate
, moderate 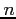 , and large
, and large 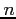 ).
).
|
|
Cem Ozdogan
2010-05-10
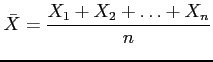
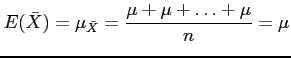
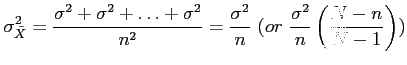
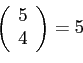 ways of making combinations.
ways of making combinations.