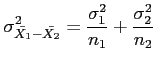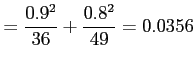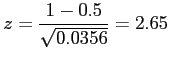- Example 8.6: An electric firm manufactures light bulbs that have a length of life that is approximately normally distributed, with mean equal to 800 hours and a standard deviation of 40 hours.
- Find the probability that a random sample of 16 bulbs will have an average life of less than 775 hours.
- Solution:
- Even though
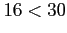 , the central limit theorem can be used because it is stated that the population distribution is approximately normal.
, the central limit theorem can be used because it is stated that the population distribution is approximately normal.
- The sampling distribution of
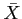 will be approximately normal, with
will be approximately normal, with
Figure 1:
Area for Example 8.6.
|
|
- Example 8.7: A engineer conjectures that the population mean of a certain component parts is 5.0 millimeters. An experiment is conducted in which 100 parts produced by the process are selected randomly and the diameter measured on each.
- It is known that the population standard deviation
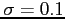 . The experiment indicates a sample average diameter
. The experiment indicates a sample average diameter
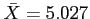 millimeters.
millimeters.
- Does this sample information appear to support or refute the engineer's conjecture?
- Solution:
Strongly refutes the conjecture!
Figure 2:
Area for Example 8.7.
|
|
- Theorem 8.3:

- Example 8.8: Two independent experiments are being run in which two different types of paints are compared.
- Eighteen specimens are painted using type
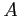 and the drying time in hours is recorded on each. The same is done with type
and the drying time in hours is recorded on each. The same is done with type 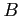 .
.
- The population standard deviations are both known to be 1.0. Assuming that the mean drying time is equal for the two types of paint,
- find
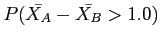 where
where 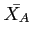 and
and 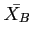 are average drying times for samples of size
are average drying times for samples of size
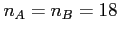 .
.
- Solution:
Figure 3:
Area for Example 8.8.
|
|
Low probability. Assumption?
Solution: Since both 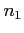 and
and 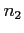 is greater than 30, the sampling distribution of
is greater than 30, the sampling distribution of
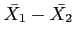 will be approximately normal.
will be approximately normal.
Low probability value.
Figure 4:
Area for Example 8.9.
|
|
Cem Ozdogan
2010-05-17
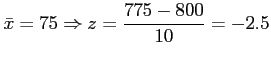
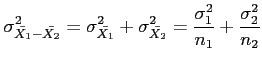

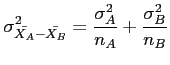
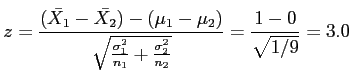
![]() and
and ![]() is greater than 30, the sampling distribution of
is greater than 30, the sampling distribution of
![]() will be approximately normal.
will be approximately normal.