-distribution

The 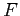-distribution finds enormous application in comparing sample variances.
Theorem 8.6:
$\fbox{\parbox{5in}{ Let $U$\ and $V$\ be two independent random variables having... ...extbf{$F$-distribution} with $\nu_1$\ and $\nu_2$\ degrees of freedom (d.f.). }}$

**Figure 9:** Typical F-distributions.
$\includegraphics[scale=0.7]{figures/08-22}$

**Figure 10:** Illustration of the 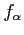$f_{\alpha }$ for the 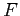-distribution.
$\includegraphics[scale=0.6]{figures/08-23}$

Theorem 8.7:
$\fbox{\parbox{5in}{ Writing $f_{\alpha}(\nu_1,\nu_2)$\ for $f_{\alpha}$\ with $\... ... f_{1-\alpha}(\nu_1,\nu_2)=\frac{1}{f_{\alpha}(\nu_2,\nu_1)} \end{displaymath}}}$
E.g., -value with 6 and 10 degrees of freedom, leaving an area of 0.95 to the right,

$\displaystyle f_{0.95}(6,10)=\frac{1}{f_{0.05}(10,6)}=\frac{1}{4.06}=0.246$
-distribution with two sample variances. Suppose that random samples of size and are selected from two normal populations with variances $\sigma_1^2$ and $\sigma_2^2$

$\displaystyle X_1^2=\frac{(n_1-1)S_1^2}{\sigma_1^2}~and~X_2^2=\frac{(n_2-1)S_2^2}{\sigma_2^2}~(from~Theorem~8.4)$
Let and having chi-squared distribution with $\nu_1=n_1-1$ and $\nu_2=n_2-1$ degrees of freedom.
Using Theorem 8.6, we obtain the following result (theorem:)

Theorem 8.8: If and are the variances of independent random samples of size and taken from normal populations with variances $\sigma_1^2$ and $\sigma_2^2$ , respectively, then

$\displaystyle F=\frac{U/\nu_1}{V/\nu_2}=\frac{S_1^2/\sigma_1^2}{S_2^2/\sigma_2^2}=\frac{\sigma_2^2S_1^2}{\sigma_1^2S_2^2}$
has an -distribution with $\nu_1=n_1-1$ and $\nu_2=n_2-1$ degrees of freedom.

What is the 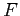-distribution used for?
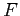-distribution is called the variance ratio distribution.
- It is used two-sample situations to draw inferences about the population variances. (Theorem 8.8)
- It is also applied to many other types of problems in which the sample variances are involved.
Suppose there are three types of paints to compare. We wish to determine if the population means are equivalent.

Sample Sample Sample

Paint Mean Variance Size

A 4.5 0.20 10

B 5.5 0.14 10

C 6.5 0.11 10

The notion of the important components of variability is best seen through some simple graphics.

**Figure 11:** Data from three distinct samples.
$\includegraphics[scale=1]{figures/08-24}$

**Figure 12:** Data that easily could have come from the same population.
$\includegraphics[scale=1]{figures/08-25}$

Two key sources of variability:
1. Variability within samples.
2. Variability between samples.
Clearly, if 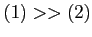, the data could all have come from a common distribution.
The above two sources of variability generate important ratios of sample variances, which are used in conjunction with the 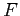-distribution.
The general procedure involved is called analysis of variance.

Cem Ozdogan 2010-05-17