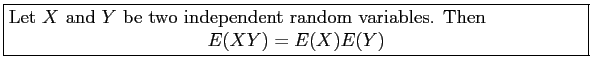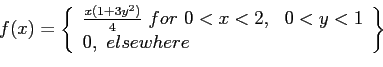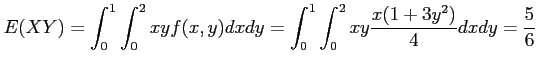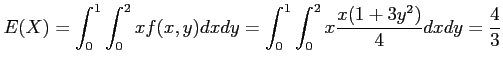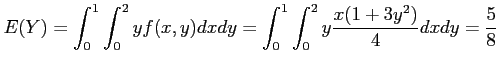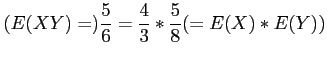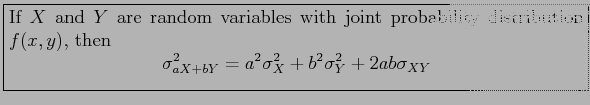- Some useful properties that will simplify the calculations of means and variances of random variables.
- These properties will permit us to deal with expectations in terms of other parameters that are either known or are easily computed.
- Theorem 4.5:
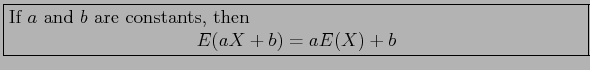
- Corollary 4.1:
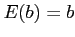
- Corollary 4.2:
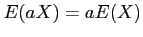
- Example 4.16: Applying Theorem 4.5 to the continuous random variable
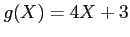 , the density function of
, the density function of 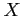 is as follows.
is as follows.
- Solution:
- Theorem 4.6:
![\fbox{\parbox{5in}{
\begin{displaymath}
E[g(X)\pm h(X)]=E[g(X)] \pm E[h(X)]
\end{displaymath}}}](img61.png)
- Theorem 4.9:

- Corollary 4.6:
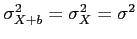
- The variance is unchanged if a constant is added to or subtracted from a random variable.
- The addition or subtraction of a constant simply shifts the values of
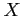 to the right/left but does not change their variability.
to the right/left but does not change their variability.
- Corollary 4.7:
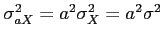
- The variance is multiplied or divided by the square of the constant.
- Theorem 4.10:
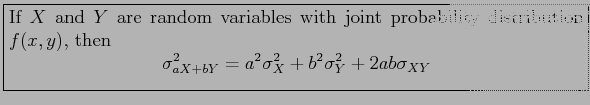
- Corollary 4.8: If
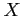 and
and 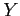 are independent random variables, then
are independent random variables, then
- Corollary 4.9: If
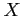 and
and 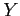 are independent random variables, then
are independent random variables, then
- Corollary 4.10: If
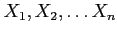 are independent random variables, then
are independent random variables, then
- Example 4.20:
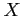 and
and 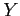 are random variables with variances
are random variables with variances
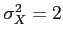 ,
,
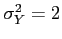 , and covariance
, and covariance
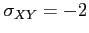 ,
,
- Find the variance of the random variable
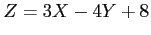
- Solution:
- Example 4.21: Let
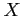 and
and 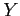 denote the amount of two different types of impurities in a batch of a certain chemical product.
denote the amount of two different types of impurities in a batch of a certain chemical product.
- Suppose that
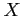 and
and 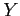 are independent random variables with variances
are independent random variables with variances
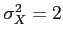 ,
,
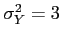
- Find the variance of the random variable
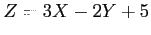
- Solution:
Cem Ozdogan
2010-03-25
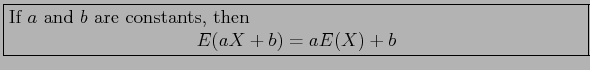
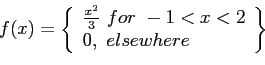
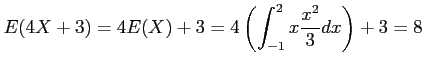
![\fbox{\parbox{5in}{
\begin{displaymath}
E[g(X)\pm h(X)]=E[g(X)] \pm E[h(X)]
\end{displaymath}}}](img61.png)
![\fbox{\parbox{5in}{
\begin{displaymath}
E[g(X,Y)\pm h(X,Y)]=E[g(X,Y)] \pm E[h(X,Y)]
\end{displaymath}}}](img62.png)