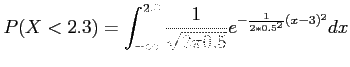- The most important continuous probability distribution in the entire field of statistics is the normal distribution.
- The normal curve describes approximately many phenomena that occur in nature, industry and research (human height, measurement errors, stock market!, etc.).
- In 1733, Abraham DeMoivre developed the mathematical equation of the normal curve.
- The normal distribution is often referred to as the Gaussian distribution, in honour of Karl Friedrich Gauss (1777-1855), who also derived its equation from a study of errors in repeated measurements of the same quantity.
- The term normal distribution is a historical accident because there is nothing particularly normal about the normal distribution and nor is there anything abnormal about other distribution.
Figure 3:
Normal curves with
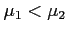 and
and
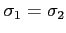 .
.
|
|
Figure 4:
Normal curves with
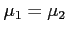 and
and
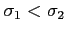 .
.
|
|
Figure 5:
Normal curves with
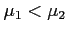 and
and
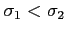 .
.
|
|
The properties of the normal curve
- The mode, which is the point on the horizontal axis where the curve is a maximum, occurs at
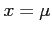 .
.
- The curve is symmetric about a vertical axis through the mean
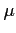 .
.
- The curve has its points of inflection at
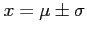 , is concave downward if
, is concave downward if
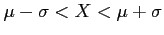 , and is concave upward otherwise.
, and is concave upward otherwise.
- The normal curve approaches the horizontal axis asymptotically as we proceed in either direction away from the mean.
- The total area under the curve and above the horizontal axis is equal to 1.
- Both tails become dramatically thin beyond
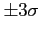 from the mean
from the mean 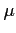 .
.
- A certain type of battery lasts on average3 years with a standard deviation of 0.5 years.
- Assuming battery lives are normally distributed,
- Find the probability that a given battery will last less than 2.3 years;
- Solution:
- Difficult to solve!
- Then, tabulation of normal curve areas is necessary.
Cem Ozdogan
2010-04-21
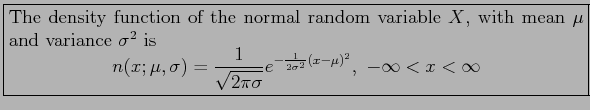
![]() having the bell-shaped distribution of Fig. 2 is called a normal random variable.
having the bell-shaped distribution of Fig. 2 is called a normal random variable.