Next: About this document ...
>> format long
>> x=-3:0.1:3
>> fzero('x.^3-x-2',[-3 3])
ans = 1.521379706804568
>> x=-3:0.1:3;
>> plot(x,x.^3-x-2);grid on;
>> x2=1.0;
>> x0=1.2;
>> x1=1.4;
>> h2=x0-x2;
>> gamma=h2/h1;
>> fn=inline('x.^3-x-2');
>> c=feval(fn,x0);
>> a=(gamma*feval(fn,x1)-feval(fn,x0)*(1+gamma)+feval(fn,x2))
/(gamma*h1^2*(1+gamma));
>> b=(feval(fn,x1)-feval(fn,x0)-a*h1^2)/h1;
>> nu=(2*c)/(b+sqrt(b^2-4*a*c));
>> root=x0-nu
%%%
>> x2=1.2;
>> x0=1.4;
>> x1=1.524956139135861;
>> h1=x1-x0;
>> h2=x0-x2;
>> gamma=h2/h1;
>> c=feval(fn,x0);
>> a=(gamma*feval(fn,x1)-feval(fn,x0)*(1+gamma)+feval(fn,x2))
/(gamma*h1^2*(1+gamma));
>> b=(feval(fn,x1)-feval(fn,x0)-a*h1^2)/h1;
>> nu=(2*c)/(b+sqrt(b^2-4*a*c));
>> root=x0-nu
%%%
>> x2=1.4;
>> x0=1.521356085625905;;
>> x1=1.524956139135861;
>> h1=x1-x0;
>> h2=x0-x2;
>> gamma=h2/h1;
>> c=feval(fn,x0);
>> a=(gamma*feval(fn,x1)-feval(fn,x0)*(1+gamma)+feval(fn,x2))
/(gamma*h1^2*(1+gamma));
>> b=(feval(fn,x1)-feval(fn,x0)-a*h1^2)/h1;
>> nu=(2*c)/(b+sqrt(b^2-4*a*c));
>> root=x0-nu
root =
1.521379705079513
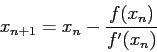
>> format long
>> x=-pi:0.1:pi
>> fzero('sin(x)-4*x+2',[0 1])
ans = 0.651618523135209
>> x=0;
>> sin(x)-4*x+2
ans = 2
>> x=1;
>> sin(x)-4*x+2
ans = -1.158529015192103
write the function
function fx=func(x)
fx=sin(x)-4*x+2;
save as func.m
write the function
function fx=funcdiff(x)
fx=cos(x)-4;
save as funcdiff.m
The best choice for >> x0=0;x0-(func(x0)/funcdiff(x0)) ans = 0.6667 (0.666666666666667) >> x0=0.6667;x0-(func(x0)/funcdiff(x0)) ans = 0.6516 (0.651640263601115) >> x0=0.6516;x0-(func(x0)/funcdiff(x0)) ans = 0.6516 (0.651618523167672)or start with
>> x0=1;x0-(func(x0)/funcdiff(x0)) ans = 0.6651 (0.665135766874333) >> x0=0.6651;x0-(func(x0)/funcdiff(x0)) ans = 0.6516 (0.651635876939131) >> x0=0.6516;x0-(func(x0)/funcdiff(x0)) ans = 0.6516 (0.651618523167672)
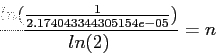
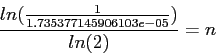
![\begin{displaymath}
A=\left[
\begin{array}{rrrr}
1 & 3 & 1 & 1 \\
2 & 5 & 2 &...
...egin{array}{r}
6 \\
2 \\
4 \\
3 \\
\end{array} \right]
\end{displaymath}](img34.png)
>> A=[1 3 1 1; 2 5 2 2; -1 -3 -3 5; 1 3 2 2]
>> b=[6 2 4 3]
>> format short
>> GEPivShow(A,b')
Begin forward elmination with Augmented system:
1 3 1 1 6
2 5 2 2 2
-1 -3 -3 5 4
1 3 2 2 3
Swap rows 1 and 2; new pivot = 2
After elimination in column 1 with pivot = 2.000000
2.0000 5.0000 2.0000 2.0000 2.0000
0 0.5000 0 0 5.0000
0 -0.5000 -2.0000 6.0000 5.0000
0 0.5000 1.0000 1.0000 2.0000
After elimination in column 2 with pivot = 0.500000
2.0000 5.0000 2.0000 2.0000 2.0000
0 0.5000 0 0 5.0000
0 0 -2.0000 6.0000 10.0000
0 0 1.0000 1.0000 -3.0000
After elimination in column 3 with pivot = -2.000000
2.0000 5.0000 2.0000 2.0000 2.0000
0 0.5000 0 0 5.0000
0 0 -2.0000 6.0000 10.0000
0 0 0 4.0000 2.0000
ans =
-21.0000
10.0000
-3.5000
0.5000
>> det(A)
ans = 8
>> 2.0000*0.5000*-2.0000*4.0000 %product of the diagonal of U
ans = 8
% For LU-decomposition
>> [L,U,pv]=luPiv(A)
L =
1.0000 0 0 0
0.5000 1.0000 0 0
-0.5000 -1.0000 1.0000 0
0.5000 1.0000 -0.5000 1.0000
U =
2.0000 5.0000 2.0000 2.0000
0 0.5000 0 0
0 0 -2.0000 6.0000
0 0 0 4.0000
pv =
2
1
3
4
% one time pivoting
% solution is completed
%**********************************************
% For proving purpose
>> A=[1 3 1 1; 2 5 2 2; -1 -3 -3 5; 1 3 2 2]
A =
1 3 1 1
2 5 2 2
-1 -3 -3 5
1 3 2 2
% our Idendity matrix becomes for swaping rows 1 and 2
>> pivoting1=[0 1 0 0; 1 0 0 0; 0 0 1 0; 0 0 0 1]
pivoting1 =
0 1 0 0
1 0 0 0
0 0 1 0
0 0 0 1
% apply this pivoting to our original matrix
>> A=pivoting1*A
A =
2 5 2 2
1 3 1 1
-1 -3 -3 5
1 3 2 2
>> [L,U,pv] = luPiv(A)
L =
1.0000 0 0 0
0.5000 1.0000 0 0
-0.5000 -1.0000 1.0000 0
0.5000 1.0000 -0.5000 1.0000
U =
2.0000 5.0000 2.0000 2.0000
0 0.5000 0 0
0 0 -2.0000 6.0000
0 0 0 4.0000
pv =
1
2
3
4
% it is proved.
%**********************************************
% for not pivoting case;
>> GEshow(A,b')
Begin forward elmination with Augmented system:
1 3 1 1 6
2 5 2 2 2
-1 -3 -3 5 4
1 3 2 2 3
After elimination in column 1 with pivot = 1.000000
1 3 1 1 6
0 -1 0 0 -10
0 0 -2 6 10
0 0 1 1 -3
After elimination in column 2 with pivot = -1.000000
1 3 1 1 6
0 -1 0 0 -10
0 0 -2 6 10
0 0 1 1 -3
After elimination in column 3 with pivot = -2.000000
1 3 1 1 6
0 -1 0 0 -10
0 0 -2 6 10
0 0 0 4 2
ans =
-21.0000
10.0000
-3.5000
0.5000
% Solutions are the same. They are same because the system is
% not ill-conditioned.