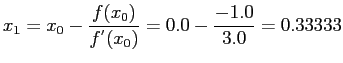- Newton's algorithm is widely used because, it is more rapidly convergent than any of the methods discussed so far. Quadratically convergent
- The error of each step approaches a constant K times the square of the error of the previous step.
- The number of decimal places of accuracy nearly doubles at each iteration.
- When Newton's method is applied to
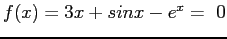 , if we begin with
, if we begin with 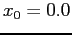 :
:
- After three iterations, the root is correct to seven digits (.3604217029603
2440136932951583028); convergence is much more rapid than any previous method.
- In fact, the error after an iteration is about one-third of the square of the previous error.
- There is the need for two functions evaluations at each step,
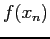 and
and 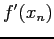 and we must obtain the derivative function at the start.
and we must obtain the derivative function at the start.
- If a difficult problem requires many iterations to converge, the number of function evaluations with Newton's method may be many more than with linear iteration methods.
- Because Newton's method always uses two per iteration whereas the others take only one.
- An algorithm for the Newton's method :
- The method may converge to a root different from the expected one or diverge if the starting value is not close enough to the root.
- In some cases Newton's method will not converge (Fig. 3.7).
Figure 3.7:
Graphical illustration of the case that Newton's Method will not converge.
|
|
- Starting with
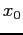 , one never reaches the root
, one never reaches the root 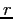 because
because 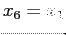 and we are in an endless loop.
and we are in an endless loop.
- Observe also that if we should ever reach the minimum or maximum of the curve, we will fly off to infinity.
- Example: Apply Newton's method to
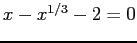 .
.
(http://siber.cankaya.edu.tr/ozdogan/NumericalComputations/mfiles/chapter1/demoNewton.m m-file: demoNewton.m.
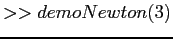
- Example: A general implementation of Newton's method.
(http://siber.cankaya.edu.tr/ozdogan/NumericalComputations/mfiles/chapter1/newton.m m-files: newton.m),(http://siber.cankaya.edu.tr/ozdogan/NumericalComputations/mfiles/chapter1/fx3n.m fx3n.m).
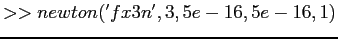
Cem Ozdogan
2011-12-27