Approximation of Functions
- To get the value of
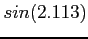 or
or 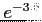 .
.
- Does NOT look up in tables and interpolate!
- The computer approximates every function from some polynomial that is customized to give the values very accurately.
- We want the approximation to be efficient in that it obtains the values with the smallest error in the least number of arithmetic operations.
- Another way to approximate a function is with a series of sine and cosine terms, Fourier series (represents periodic functions).
- Chebyshev Polynomials and Chebyshev Series: Chebyshev polynomials are orthogonal polynomials that are the basis for fitting nonalgebraic functions with maximum efficiency.
- They can be used to modify a Taylor series so that there is greater efficiency.
- A series of such polynomials converges more rapidly than a Taylor series.
- Fourier Series: These are series of sine and cosine terms that can be used to approximate a function within a given interval very closely, even functions with discontinuities.
- Fourier series are important in many areas, particularly in getting an analytical solution to partial-differential equations.
- If we want to represent a known function as a polynomial, one way to do it is with a Taylor series.
- Given a function,
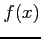 , we write
, we write
- Where
- Then, rewriting this Taylor series expansion as
- Unless
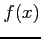 is itself a polynomial, the series may have an infinite number of terms.
is itself a polynomial, the series may have an infinite number of terms.
- Terminating the series incurs an error, truncation error.
- The error after the
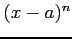 term,
term,
Subsections
Cem Ozdogan
2010-12-19
![\begin{displaymath}
Error=\frac{(x-a)^{n+1}}{(n+1)!}f^{(n+1)}(\xi),where~ \xi~in~[a,x]
\end{displaymath}](img10.png)