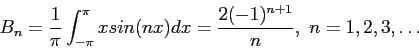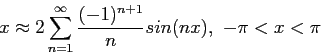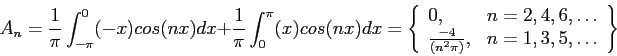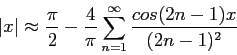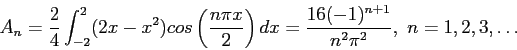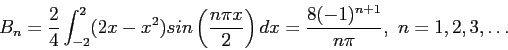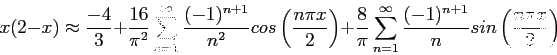Fourier Series for Periods Other Than 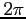
Figure 2:
Left: Plot of 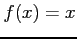 , periodic of period
, periodic of period 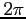 ,Right: Plot of the Fourier series expansion for
,Right: Plot of the Fourier series expansion for 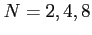 .
.
|
|
Examples:
- Let
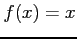 be periodic between
be periodic between 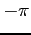 and
and 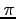 . (See Figure 2left). Find the
. (See Figure 2left). Find the 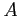 s and
s and 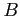 s of its Fourier expansion. For
s of its Fourier expansion. For 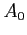 ;
;
For the other  s;
s;
For the other  s;
s;
We then have
Figure 2right shows how the series approximates to the function when only two, four, or eight terms are used.
- Find the Fourier coefficients for
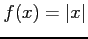 on
on 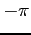 to
to 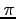 ;
;
Because the definite integrals are nonzero only for odd values of 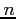 , it simplifies to change the index of the summation. The Fourier series is then
, it simplifies to change the index of the summation. The Fourier series is then
Figure 3 shows how the series approximates the function when two, four, or eight terms are used.
Figure 3:
Plot of Fourier series for 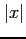 for
for 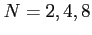 .
.
|
|
- Find the Fourier coefficients for
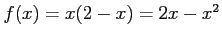 over the interval [-2, 2] if it is periodic of period 4. Equations 7 and 8 apply.
over the interval [-2, 2] if it is periodic of period 4. Equations 7 and 8 apply.
Figure 4 shows how the series approximates to the function when 40 terms are used.
Figure 4:
Plot of Fourier series for 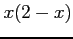 for
for 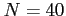 .
.
|
|
With MATLAB,
Cem Ozdogan
2010-12-29
![\begin{displaymath}
A_0=\frac{1}{\pi}\int_{-\pi}^{\pi} f(x)dx=\frac{1}{\pi}\int_{-\pi}^{\pi} xdx=\left[ \frac{x^2}{2\pi}\right] ^{\pi}_{-\pi}=0
\end{displaymath}](img56.png)