Next: Solving Nonlinear Equations Up: Preliminaries Previous: Polynomials Contents
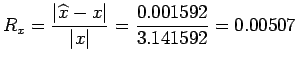
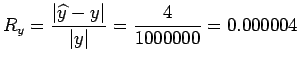
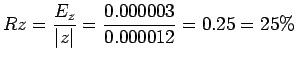
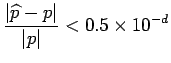
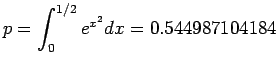
![$\displaystyle \widehat{p} = \int_0^{1/2}P_8(x)dx = \left[x+ \frac{x^3}{3}+\frac{x^5}{5(2)!}+\frac{x^7}{7(3)!}+\frac{x^9}{9(4)!}\right]_0^{1/2}
= 0.544986720817
$](img154.png)
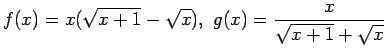
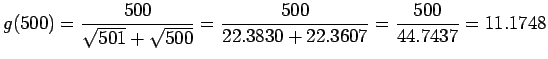
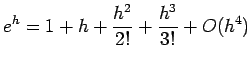
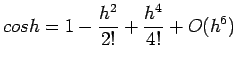
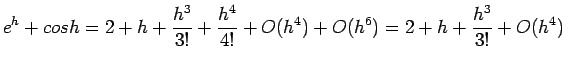
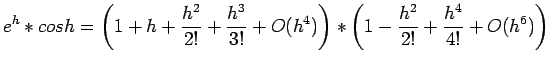
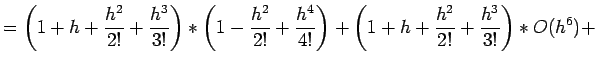
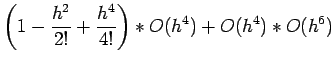
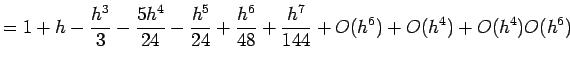
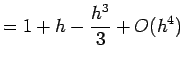
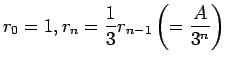
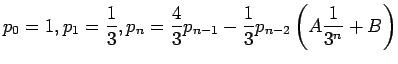
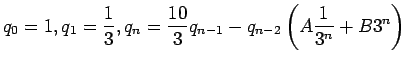
% Determines effective machine precision for MATLAB
a = 1.0 ;
while ( (1. + a) ~= 1)
a = a/2. ;
end
delta = 2.0*a ;
sprintf(' Machine Precision of MATLAB is %9.2e', delta )
% uses the MATLAB chop.m function to find simulated machine
% precision for a NDIGITS decimal ( base 10 ) machine.
data = [] ;
for NDIGITS = 2: 20 ;
a = 1.0 ;
while ( chop( (1.+a), NDIGITS ) ~= chop( (1.+a/2.), NDIGITS) )
a = chop( a/2. , NDIGITS) ;
end
theoret = 0.5*10^(1-NDIGITS) ;
data = [ data ; NDIGITS (1.5)*a theoret ] ;
end
% Note the use of (semi)logarithmic plots is usually preferable
% for displaying error behavior.
semilogy( data(:,1) , data(:,2) , '*', ...
data(:,1) , data(:,3) ) ;
xlabel('NDIGITS');
ylabel('Machine Precision')
legend('Observed','Theoretical');
title('Dependence of Machine Precision on Machine "Size"');
% Determines the accuracy of a computed expression which is potentially
% subject to cancellation errors, using the MATLAB chop.m function.
clear ;
data = [] ;
NDIGITS = 8 ;
mu_NDIGITS = 0.5*10^(1-NDIGITS) ;
mu_calc = 50*mu_NDIGITS ;
for n = 1: 30 ;
x = 2^n ;
xsing = chop( x , NDIGITS ) ;
xm1_sing = chop( xsing - 1 , NDIGITS ) ;
xsq_sing = chop( xsing*xsing , NDIGITS) ;
xsqp4_sing = chop( xsq_sing + 4 , NDIGITS ) ;
sroot_sing = chop( sqrt( xsqp4_sing ) , NDIGITS ) ;
fval_sing = chop( sroot_sing - xm1_sing , NDIGITS ) ;
f_double = sqrt( x^2 + 4 ) - ( x - 1 ) ;
rel_err = abs( f_double - fval_sing )/abs(f_double + eps ) + eps ;
data = [ data ; x rel_err f_double fval_sing] ;
end
xmin = min(data(:,1)) ; xmax = max(data(:,1)) ;
loglog( data(:,1) , data(:,2) , '-.' , ...
[ xmin xmax ] , [ mu_calc mu_calc ] , ':' ) ;
axis( [ xmin 10*xmax 10^(-10) 10^3 ] );
xlabel( 'x' ) ; ylabel( 'Relative Difference') ;
legend('Observed','"Acceptable"');
title('Variation of the Accuracy of a Computed Function with x');
figure(2);
semilogx( data(:,1), data(:,3), data(:,1), data(:,4),':');
xlabel('x') ; ylabel('Computed Value of f(x)')
axis([min(data(:,1)), 10*max(data(:,1)),-.25, 2.25])
legend('Double Precision','Single Precision');
title('Effect of Machine Precision on the Accuracy of a Computed Function')
a=123*2*pi*/360
L=inline('9/sin(pi-2.1468-c)+7/sin(c)')
fplot(L,[0.4,0.5]); grid on
fminbnd(L,0.4,0.5)
L(0.4677)
fminbnd(L,0.4,0.5,optimset('Display','iter'))
k=0.0; j=0.0001; for l=1:10000 k=k+j; end k k=0.0; j=0.0001; a=single(k); b=single(j); for l=1:10000 a=a+b; end
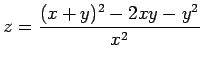
x=0.01; y=10000;z=((x+y)^2-2*x*y-y^2)/x^2; x=0.001; y=10000;z=((x+y)^2-2*x*y-y^2)/x^2 x=0.0001; y=10000;z=((x+y)^2-2*x*y-y^2)/x^2 x=0.00001; y=10000;z=((x+y)^2-2*x*y-y^2)/x^2 x=0.000001; y=10000;z=((x+y)^2-2*x*y-y^2)/x^2 x=0.0000001; y=10000;z=((x+y)^2-2*x*y-y^2)/x^2