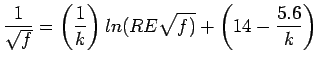''solve 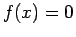 '' where
'' where 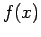 is a function of
is a function of 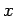 . The values of
. The values of 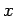 that make
that make 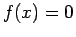 are called the roots of the equation.
They are a1so called the zeros of
are called the roots of the equation.
They are a1so called the zeros of 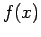 .
.
The following non-linear equation can compute the friction factor,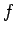 :
:
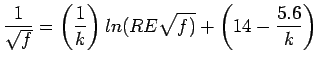
where the parameter 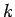 is known and RE, the so-called Reynold's number. The equation for
is known and RE, the so-called Reynold's number. The equation for
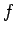 is not solvable except by the numerical procedures of this chapter.
is not solvable except by the numerical procedures of this chapter.
- Interval Halving (Bisection). Describes a method that is very simple and foolprof but is not very efficient. We examine how the error decreases as the method continues.
- Linear Interpolation Methods. Tells how approximating the function in the vicinity of the root with a straight line can find a root more efficiently. It has a better "rate of convergence".
- Newton's Method. Explains a still more efficient method that is very widely used but there are pitfalls that you should know about. Complex roots can be found if complex arithmetic is employed.
- Muller's Method. Approximates the function with a quadratic polynomial that fits to the function better than a straight line. This significantly improves the rate of convergence over linear interpolation.
- Fixed-Point Iteration:
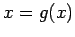 Method. Uses a different approach: The function
Method. Uses a different approach: The function 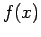 is rearranged to an equivalent form,
is rearranged to an equivalent form, 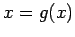 . A starting value,
. A starting value, 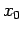 , is substituted into
, is substituted into 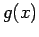 to give a new x-value,
to give a new x-value, 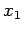 . This in turn is used to get another x-value. If the function
. This in turn is used to get another x-value. If the function 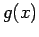 is properly chosen, the successive values converge.
is properly chosen, the successive values converge.
Subsections
2004-12-28