Linear Interpolation (False Position)

A way to avoid such pathology is to ensure that the root is bracketed between the two starting values and remains between the successive pairs. When this is done, the method is known as linear interpolation
This technique is similar to bisection except the next iterate is taken at the intersection of a line between the pair of x-values and the x-axis rather than at the midpoint.
Doing so gives faster convergence than does bisection, but at the expense of a more complicated algorithm.

An algorithm for the method of false position (regula falsi):
$\fbox{\parbox{10cm}{ To determine a root of $f(x) = 0$, given two values of $x_0... ...\\ Set $x_0= x_2$\\ End If\\ Until $\vert f(x_2)\vert<tolerance value$.\\ }}$

**Table 3.3:** Comparison of methods, 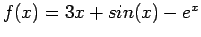, starting from .
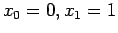$\begin{table} \begin{center} \includegraphics[scale=1]{figures/1.6.ps} \end{center}\end{table}$

If 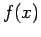is not continuous, the method may fail.
Table 3.3 compares the results of three methods-interval halving (bisection), linear interpolation, and the secant method-on
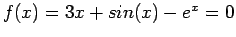
Observe that the speed of convergence is best for the secant method, poorest for interval halving, and intermediate for false position.

2004-12-28