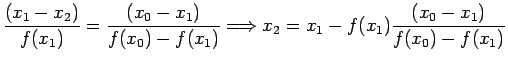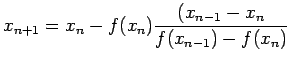The Secant Method

Figure 3.2: Graphical illustration of the Secant Method.

• The secant method begins by finding two points on the curve of $f(x)$, hopefully near to the root we seek.
• As Figure 3.2 illustrates, we draw the line through these two points and find where it intersects the x-axis.
• If $f(x)$ were truly linear, the straight line would intersect the x-axis at the root.
• The intersection of the line with the x-axis is not at $x=r$ but it should be close to it. From the obvious similar triangles we can write
  $$\frac{(x_1 - x_2)}{f(x_1)}=\frac{ (x_0 - x_1)}{f(x_0) - f(x_1)}\Longrightarrow x_2=x_1-f(x_1)\frac{(x_0-x_1)}{f(x_0)-f(x_1)}$$

• Because f(x) is not exactly linear, $x_2$ is not equal to $r$, but it should be closer than either of the two points we began with. If we repeat this, we have:
  $$x_{n+1}=x_n-f(x_n)\frac{(x_{n-1}-x_n}{f(x_{n-1})-f(x_n)}$$

• The net effect of this rule is to set $x_0 =x_1$ and $x_1=x_2$, after each iteration.
• The technique we have described is known as, the secant method because the line through two points on the curve is called the secant line.

An algorithm for the Secant Method:

Table 3.2: The Secant method for 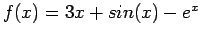$f(x)=3x + sin(x) - e^x$, starting from 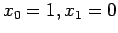$x_0=1,x_1=0$, using a tolerance value of 1E-6.

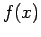• If $f(x)$ is not continuous, the method may fail.
• An alternative stopping criterion for the secant method is when the pair of points being used are sufficiently close together.
• Table 3.2 shows the results from the secant method for the same function that was used to illustrate bisection.
• An objection is sometimes raised about the secant method. If the function is far from linear near the root, the successive iterates can fly off to points far from the root, as seen if Fig. 3.3.
• If the method is being carried out by a program that displays the successive iterates, the user can interrupt the program should such improvident behavior be observed. Also, if the function was plotted before starting the method, it is unlikely that the problem will be encountered, because a better starting value would be used.

Figure 3.3: A pathological case for the secant method.