- We have given the following function;
Look at to the plot of the function to learn where the function crosses the x-axis. MATLAB can do it for us:
>> fx = inline ( ' 3 *x + sin ( x) - exp ( x) ')
>> fplot ( fx, [ 0 2 ]) ; grid on
An algorithm for Halving the Interval (Bisection):

The MATLAB program for this algorithm is given.
function rtn=bisec(fx,xa,xb,n)
%bisec does n bisections to approximate
% a root of fx
x=xa; fa=eval(fx);
x=xb; fb=eval(fx);
for i=1:n;
xc=(xa+xb)/2; x=xc; fc=eval(fx);
X=[i,xa,xb,xc,fc];
disp(X);
if fc*fa<0
xb=xc;
else xa=xc;
end
end
save with the name bisec.m. Then;
>> fx=inline(' 3 *x + sin ( x) - exp ( x) ');
>> bisec(fx,0,1,13)
Modify this MATLAB program for the bisection method for using a tolerance value of 1E-4.
function [c,err,yc]=bisect(f,a,b,delta)
%Input - f is the function input as a string 'f'
% - a and b are the left and right endpoints
% - delta is the tolerance
%Output - c is the zero
% - yc= f(c)
% - err is the error estimate for c
% format long;
disp('iteration xa xb xc f(c)')
ya=feval(f,a);
yb=feval(f,b);
if ya*yb > 0,break,end
max1=1+round((log(b-a)-log(delta))/log(2));
for k=1:max1
c=(a+b)/2;
yc=feval(f,c);
if yc==0
a=c;
b=c;
elseif yb*yc>0
b=c;
yb=yc;
else
a=c;
ya=yc;
end
X=[k,a,b,c,yc];
disp(X);
if b-a < delta, break,end
end
c=(a+b)/2;
err=abs(b-a);
yc=feval(f,c);
save with the name bisect.m. Then;
>> fx=inline(' 3 *x + sin ( x) - exp ( x) ');
>> [c,err,yc]=bisect(fx,0,1,10^4)
>> [c,err,yc]=bisect(fx,1,2,10^4)
- Use the function used in the previous item, and write a MATLAB program for the method of false position (regula falsi):
An algorithm for the method of false position (regula falsi):

function [c,err,yc]=regula(f,a,b,delta,epsilon,max1)
%Input - f is the function input as a string 'f'
% - a and b are the left and right endpoints
% - delta is the tolerance for the zero
% - epsilon is the tolerance for the value of f at the zero
% - max1 is the maximum number of iterations
%Output - c is the zero
% - yc=f(c)
% - err is the error estimate for c
%format long;
disp('iteration xa xb xc f(c) dx')
ya=feval(f,a);
yb=feval(f,b);
if ya*yb>0
disp('Note: f(a)*f(b) >0'),
break,
end
for k=1:max1
dx=yb*(b-a)/(yb-ya);
c=b-dx;
ac=c-a;
yc=feval(f,c);
if yc==0,break;
elseif yb*yc>0
b=c;
yb=yc;
else
a=c;
ya=yc;
end
dx=min(abs(dx),ac);
X=[k,a,b,c,yc,dx];
disp(X);
if abs(dx)<delta,break,end
if abs(yc)<epsilon, break,end
end
c;
err=abs(b-a)/2;
yc=feval(f,c);
save with the name regula.m. Then;
>> fx=inline(' 3 *x + sin ( x) - exp ( x) ');
>> [c,err,yc]=regula(fx,0,1,10^4,10^-4,14)
>> [c,err,yc]=regula(fx,1,2,10^4,10^-4,14)
- To obtain the true value for the root
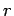 , which is needed to compute the actual error. MATLAB surely used a more advanced method than bisection.
, which is needed to compute the actual error. MATLAB surely used a more advanced method than bisection.
>> solve('3*x + sin(x) - exp(x)')
ans=
.36042170296032440136932951583028
Tabulate the actual error values as the following;
Table 3.4:
The Error Sequences
| n |
Bisection 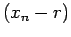 |
Regula Falsi 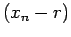 |
Bisection 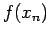 |
Regula Falsi 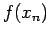 |
| 1 |
|
|
|
|
| 2 |
|
|
|
|
| 3 |
|
|
|
|
| 4 |
|
|
|
|
| 5 |
|
|
|
|
| 6 |
|
|
|
|
| 7 |
|
|
|
|
| 8 |
|
|
|
|
| 9 |
|
|
|
|
| 10 |
|
|
|
|
| 12 |
|
|
|
|
| 13 |
|
|
|
|
| 14 |
|
|
|
|
| 15 |
|
|
|
|
|
function bisectregula(f,a,b,delta,epsilon)
%Input - f is the function input as a string 'f'
% - a and b are the left and right endpoints
% - delta is the tolerance
% - epsilon is the tolerance for the value of f at the zero
% - max1 is the maximum number of iterations
%Output - c is the zero
% - yc= f(c)
% - err is the error estimate for c
% format long;
disp(' Bisection Regula Bisection Regula')
disp('iteration (x-r) (x-r) f(x) f(x)')
ya=feval(f,a);
yb=feval(f,b);
if ya*yb>0
disp('Note: f(a)*f(b) >0'),
break,
end
realroot=0.36042170296032440136932951583028;
max1=1+round((log(b-a)-log(delta))/log(2));
aa=a;
bb=b;
ybb=yb;
yaa=ya;
for k=1:max1
c=(a+b)/2;
yc=feval(f,c);
if yc==0
a=c;
b=c;
elseif yb*yc>0
b=c;
yb=yc;
else
a=c;
ya=yc;
end
e_b=realroot-c;
f_b=yc;
dx=ybb*(bb-aa)/(ybb-yaa);
c=bb-dx;
ac=c-aa;
yc=feval(f,c);
if yc==0,break;
elseif ybb*yc>0
bb=c;
ybb=yc;
else
aa=c;
yaa=yc;
end
dx=min(abs(dx),ac);
e_r=realroot-c;
f_r=yc;
X=[k,e_b,e_r,f_b,f_r];
disp(X);
if b-a < delta, break,end
% if abs(dx)<delta,break,end
% if abs(yc)<epsilon, break,end
end
save with the name bisectregula.m. Then;
>> fx=inline(' 3 *x + sin ( x) - exp ( x) ');
>> bisectregula(fx,0,1,10^4,10^-4)

