- The fixed-point method converges at a linear rate; it is said to be linearly convergent, meaning that the error at each successive iteration is a constant fraction of the previous error. (Actually, this is true only as the errors approach zero.)
- If we tabulate the errors after each step in getting the roots of the polynomial and its ratio to the previous error, we find that the magnitudes of the ratios to be leveling out at 0.3333. (See Fig. 3.5)
Table 3.5:
The order of convergence for the iteration algorithm with the different forms of 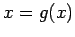 .
.
![\begin{table}
\begin{center}
\includegraphics[scale=1]{figures/1.15.ps}
\end{center}\end{table}](img294.png) |
2004-12-28