Figure 3.10:
Left: The curve on the left has a triple root at 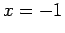 [the function is
[the function is 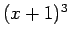 ]. The curve on the right has a double root at
]. The curve on the right has a double root at 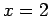 [the function is
[the function is 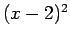 ].Right: Plot of
].Right: Plot of
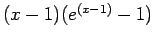 .
.
|
- A function can have more than one root of the same value. See Fig. 3.10left.
- The methods we have described do not work well for multiple roots. For example, Newton's method is only linearly convergent at a double root.
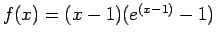 has a double root at
has a double root at 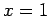 , as seen in Fig. 3.10right.
, as seen in Fig. 3.10right.
- Table 3.6left gives the errors of successive iterates and the convergence is clearly linear.
- When Newton's method is applied to a triple root, convergence is still linear, as seen in Table 3.6right. With a triple root, the ratio of errors is larger, about
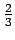 , compared to
, compared to
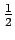 for the double root of Table 3.6left.
for the double root of Table 3.6left.
Table 3.6:
Right: Errors when finding a double root. Left: Successive errors with Newton's method, for
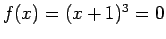 .
.
![\includegraphics[scale=0.85]{figures/1.18.ps}](img300.png) |
![\includegraphics[scale=0.85]{figures/1.19.ps}](img301.png) |
2004-12-28
![\includegraphics[scale=0.85]{figures/1.18.ps}](img300.png)
![\includegraphics[scale=0.85]{figures/1.19.ps}](img301.png)