- We have given the following function;
- To obtain the true value for the root
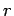 , which is needed to compute the actual error. MATLAB is used as:
, which is needed to compute the actual error. MATLAB is used as:
>> solve('3*x + sin(x) - exp(x)')
ans=
.36042170296032440136932951583028
- Use the function used in the previous item, and write a MATLAB program for Muller's method:
An algorithm for Muller's method :

function [k,x,y,err,S,F]=muller(f,x2,x0,x1,delta,epsilon,max1)
%Input - f is the object function input as a string 'f'
% x0, x1, and x2 are the initial approximations
% - delta is the tolerance for x0, x1, and x2
% - epsilon the the tolerance for the function values f
% - max1 is the maximum number of iterations
%Output - k is the number of iterations that were carried out
% - x is the Muller approximation to the zero of f
% - y is the function value y = f(x)
% - err is the error in the approximation of x.
% - S' contains the sequence {x}
% - F' contains the sequence {f(x)}
format short;
%format long;
disp('iteration x2 x0 x1 f(x0)')
%Initalize the matrices X and Y
X=[x2 x0 x1];
y=feval(f,x0);
D=[0,X,y];
disp(D);
Y=feval(f,X);
for k=1:max1
h1=x1-x0;
h2=x0-x2;
G=h2/h1;
c=Y(2);
a=(G*Y(3)-Y(2)*(1+G)+Y(1))/(G*h1*h1*(1+G));
b=(Y(3)-Y(2)-a*h1*h1)/h1;
%Suppress any complex roots
if b^2-4*a*c > 0
disc=sqrt(b^2-4*a*c);
else
disc=0;
end
%Find the closest root
if b < 0
disc=-disc;
end
z=2*c/(b+disc);
x=x0-z;
if x > x0
x2=x0;
x0=x;
else
x1=x0;
x0=x;
end
S(k)=x;
X=[x2 x0 x1];
Y=feval(f,X);
y=feval(f,x);
F(k)=y;
D=[k,X,y];
disp(D);
%Determine stopping criteria
err=abs(z);
relerr=err/(abs(x)+delta);
if (err<delta)|(relerr<delta)|(abs(y)<epsilon)
break
end
end
S=S';
F=F';
save with the name muller.m. Then;
>> fx=inline(' 3 *x + sin ( x) - exp ( x) ');
>> [x,y,err]=muller(fx,0,0.5,1,10^-4,10^-4,15)
>> [x,y,err]=muller(fx,1,1.5,2,10^-4,10^-4,15)
- Use the function used in the previous item, and write a MATLAB program for Fixed-point Iteration;
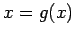 Method:
Method:
Iteration algorithm with the form 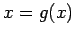

function [k,x,err,X,F] = fixedpoint(g,x0,tol,max1)
% Input - g is the iteration function
% - x0 is the initial guess for the fixed-point
% - tol is the tolerance
% - max1 is the maximum number of iterations
% Output - k is the number of iterations that were carried out
% - x is the approximation to the fixed-point
% - err is the error in the approximation
% - X'contains the sequence {x}
% - F'contains the sequence {f(x)}
%format long;
disp('iteration x g(x)')
X(1)= x0;
F(1)=feval(g,X(1));
D=[1,x0,F(1)];
disp(D);
for k=2:max1
X(k)=feval(g,X(k-1));
x=X(k);
F(k)=feval(g,X(k));
D=[k,x,F(k)];
disp(D);
err=abs(X(k)-X(k-1));
relerr=err/(abs(X(k))+eps);
if (err<tol) | (relerr<tol),break;end
end
if k == max1
disp('maximum number of iterations exceeded')
end
X=X';
F=F';
save with the name fixedpoint.m. Then;
>> gx=inline('sqrt(2*x+3)');
>> [k,x,err,X,F]=fixedpoint(gx,4,10^-4,15)
>> gx=inline('3/(x-2)');
>> [k,x,err,X,F]=fixedpoint(gx,4,10^-4,15)
>> gx=inline('log(3*x+sin(x))')
>> [k,x,err,X,F]=fixedpoint(gx,4,10^-4,15)
- Tabulate the actual error values as the following; (See Table 3.9. The number of iterations is not limited to or defined as 15.)
Table 3.9:
The Error Sequences
| n |
Muller 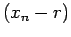 |
Fixed-point 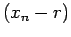 |
Muller 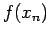 |
Fixed-point 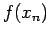 |
| 1 |
|
|
|
|
| 2 |
|
|
|
|
| 3 |
|
|
|
|
| 4 |
|
|
|
|
| 5 |
|
|
|
|
| 6 |
|
|
|
|
| 7 |
|
|
|
|
| 8 |
|
|
|
|
| 9 |
|
|
|
|
| 10 |
|
|
|
|
| 12 |
|
|
|
|
| 13 |
|
|
|
|
| 14 |
|
|
|
|
| 15 |
|
|
|
|
|
- Plot the behaviours of the errors (use ratios) for both cases. Compare and discuss the rate of convergence.
%format long;
realroot=0.36042170296032440136932951583028;
fx=inline('3*x+sin(x)-exp(x)');
[k1,x,y,err,S,F1]=muller(fx,1,1.5,2,10^-4,10^-4,15);
gx=inline('log(3*x+sin(x))');
[k2,x,err,X,F2]=fixedpoint(gx,4,10^-4,15);
if k1>k2
max1=k1;
else
max1=k2;
end
disp(' Muller Fixed-Point Muller Fixed-Point')
disp('iteration (x-r) (x-r) f(x) f(x)')
for k=1:max1
if k1>=k& k2>=k
plotyx1(k)=S(k)-realroot;
plotyx2(k)=X(k)-realroot;
plotxx1(k)=k;
plotxx2(k)=k;
D=[k,plotyx1(k),plotyx2(k),F1(k),F2(k)];
else if k1<k& k2>=k
plotyx2(k)=X(k)-realroot;
plotxx2(k)=k;
D=[k,S(k1)-realroot,plotyx2(k),F1(k1),F2(k)];
else if k1>=k& k2<k
plotyx1(k)=S(k)-realroot;
plotxx1(k)=k;
D=[k,plotyx1(k),X(k2)-realroot,F1(k),F2(k2)];
end
end
end
disp(D);
end
plot(plotxx1,plotyx1,plotxx2,plotyx2);
%plot(plotxx2,plotyx2);
save with the name main.m. Then;
>> main
For the rate of convergence: Muller's method converges much faster than fixed-point iteration.
- A pair of equations:
Solve this system by expanding both functions as a Taylor series (begin with
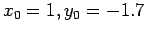 ) and by Iteration (begin with
) and by Iteration (begin with 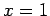 )
)
- Tabulate the actual error values as the following; (See Table 3.10. The number of iterations is not limited to or defined as 15.)
Table 3.10:
The Error Sequences
| n |
Expansion 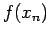 |
Iteration 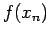 |
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 12 |
|
|
| 13 |
|
|
| 14 |
|
|
| 15 |
|
|
|

